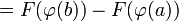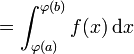- Intégration par changement de variables
-
Intégration par changement de variable
En mathématiques, le changement de variable est un procédé qui consiste à remplacer une variable ou même une fonction par une autre fonction de celle-ci ou d'un autre paramètre. Ce procédé est un des outils principaux pour la résolution d'intégrales, en analyse.
Sommaire
Principe
C'est la règle d'intégration qui découle du théorème de dérivation des fonctions composées. Soit deux fonctions dérivables f,g et sachant, par la définition d'intégrale, que
alors ce théorème permet d'obtenir
Exemple
Soit à calculer
On pose le changement de variable u = x2 et donc du = 2xdx. x varie entre
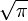 et
et 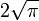 alors u varie entre π et 4π.
alors u varie entre π et 4π.Théorème
Énoncé
Soit f une fonction numérique continue, et
 une fonction de classe
une fonction de classe 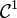 (c'est-à-dire dérivable et dont la dérivée est continue) et injective sur un intervalle [a,b] et dont l'image est contenue dans le domaine de définition de f.
(c'est-à-dire dérivable et dont la dérivée est continue) et injective sur un intervalle [a,b] et dont l'image est contenue dans le domaine de définition de f.Alors
avec
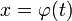
Démonstration
La fonction f étant continue, on considère une primitive F de f sur D l'ensemble de définition de f. La fonction
 est alors dérivable, comme composée de deux fonctions dérivables et on a :
est alors dérivable, comme composée de deux fonctions dérivables et on a :D'où
Changements de variables classiques
- Pour les fonctions comportant des fonctions circulaires ou hyperboliques, voir les règles de Bioche.
- Pour calculer
![\int{f\left(x, \sqrt[n]{\frac{ax+b}{cx+\mathrm d}}\right)\mathrm{\mathrm d}x}](/pictures/frwiki/102/f6426e77581bc653858a1d9e73fc15d1.png) ,
,
où f est une fraction rationnelle en deux variables, n un entier naturel et a, b, c et d quatre réels donnés, on pose
![u=\sqrt[n]{\frac{ax+b}{cx+\mathrm d}}](/pictures/frwiki/49/1a51e26e708191680c1ab84cd5ca58a6.png) :
:
le changement de variable donnera toujours une fraction rationnelle en u ; il suffit alors de la décomposer en éléments simples pour intégrer.
Cas des intégrales multiples
Losque f est une fonctions de plusieurs variables, outre le changement du domaine d'intégration on utilise le jacobien de la transformation « à la place » de
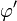 . Le jacobien est le déterminant de la matrice jacobienne. On donne ici la formulation explicite du changement de variable et le lecteur se reportera à l'article sur les intégrales multiples ou sur la matrice jacobienne pour plus de précisions sur ces notions :
. Le jacobien est le déterminant de la matrice jacobienne. On donne ici la formulation explicite du changement de variable et le lecteur se reportera à l'article sur les intégrales multiples ou sur la matrice jacobienne pour plus de précisions sur ces notions :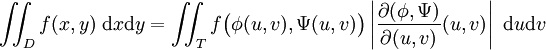 .
.
Voir aussi
- Portail des mathématiques
Catégorie : Méthode d'intégration
Wikimedia Foundation. 2010.

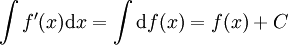
![\int \left( \frac{\mathrm d}{\mathrm d g(x)} f(g(x)) \cdot \frac{\mathrm d}{\mathrm dx} g(x) \right) \mathrm dx = \int\mathrm d[f \circ g(x)] = f \circ g (x) + C](/pictures/frwiki/53/506eb6331966a452bf10feb5304f15d2.png)
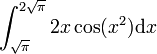
![\int_{\sqrt\pi}^{2\sqrt\pi} 2x \cos(x^2)\mathrm dx = \int_{\pi}^{4\pi} \cos(u)\mathrm du = [\sin(u)]^{4\pi}_{\pi} = \sin(4\pi)-\sin{\pi}=0-0=0](/pictures/frwiki/99/cedd5e144b188f1a44353d8e4161a0ff.png)
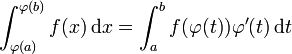
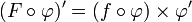
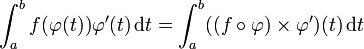
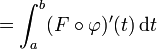
![=\left[F\circ \varphi\right]_a^b](/pictures/frwiki/52/4698c588620e67f7ee80fc986eecbfdb.png)