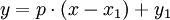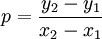- Interpolation (mathématiques)
-
Interpolation numérique
En analyse numérique (et dans son application algorithmique discrète pour le calcul numérique), l'interpolation est une opération mathématique permettant de construire une courbe à partir de la donnée d'un nombre fini de points, ou une fonction à partir de la donnée d'un nombre fini de valeurs. La solution du problème d'interpolation passe par les points prescrits, et, suivant le type d'interpolation, il lui est demandé de vérifier des propriétés supplémentaires.
Ainsi le type le plus simple d'interpolation est l'interpolation linéaire, qui consiste à "joindre les points" donnés. À partir d'une table trigonométrique, elle peut servir à estimer les valeurs situées entre les données de la table.
L'interpolation doit être distinguée de l'approximation de fonction, qui consiste à chercher la fonction la plus proche possible, selon certains critères, d'une fonction donnée. Dans le cas de l'approximation, il n'est en général plus imposé de passer exactement par les points donnés initialement. Ceci permet de mieux prendre en compte le cas des erreurs de mesure, et c'est ainsi que l'exploitation de données expérimentales pour la recherche de lois empiriques relève plus souvent de la régression linéaire, ou plus généralement de la méthode des moindres carrés.
Sommaire
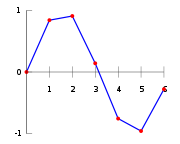
Interpolation linéaire
Article détaillé : Interpolation linéaire.Dans le cas d'une interpolation linéaire, on constitue une courbe d'interpolation qui est une succession de segments. Entre deux points p1 et p2 de coordonnées respectives (x1,y1) et (x2,y2), l'interpolation est donnée par la formule suivante
avec la pente p qui s'exprime comme
Le code C permettant d'interpoler linéairement deux valeurs dans la plage mu [0...1] est le suivant :
double interpolationLinéaire(double v1, double v2, double mu) { return(v1*(1-mu)+v2*mu); }Interpolation cubique
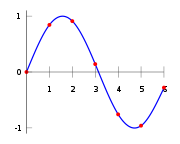
Article détaillé : Spline.Comme son nom l'indique, on utilise ici une équation cubique pour modéliser localement la courbe. Quatre points sont nécessaires pour évaluer la fonction qui remplace la courbe discrète. Tout dépend des conditions de continuité utilisées, la forme de la cubique peut varier et donner une interpolation différente (ex: interpolation cubique de Keys ou interpolation cubique splines).
Le code C permettant d'interpoler cubiquement quatre valeurs dans la plage mu [0...1] est le suivant :
double interpolationCubique(double y0,double y1,double y2,double y3,double mu) { double a0,a1,a2,a3,mu2; mu2 = mu*mu; a0 = y3 - y2 - y0 + y1; a1 = y0 - y1 - a0; a2 = y2 - y0; a3 = y1; return (a0*mu*mu2+a1*mu2+a2*mu+a3); }Interpolation polynomiale
Article détaillé : Interpolation polynomiale.Une interpolation polynomiale consiste à utiliser un polynôme unique (et non des tronçons comme précédemment), de degré aussi grand que nécessaire, pour estimer localement l'équation représentant la courbe afin de déterminer la valeur entre les échantillons.
Répartition des points d'interpolation
Pour représenter une fonction en informatique, on prend en général « un certain nombre » de points et l'on fait une interpolation polynomiale, ce qui évite de calculer trop de points. Se pose alors la question du choix des points.
Dans un premier temps, on peut prendre des points régulièrement répartis dans l'intervalle. Cependant, cela peut donner des « effets de bord » (le polynôme représente bien au milieu de l'intervalle, mais a un comportement différent aux bords bien que passant par les points), et pose problème dans les endroits où les variations de pente sont importantes.
Pour éviter les effets de bord, on utilise des points répartis selon une fonction sinusoïdale (il y a plus de points aux bords qu'au centre), voir Polynôme de Tchebychev.
On peut aussi utiliser le « remaillage automatique » : pour chaque intervalle, on calcule la différence entre le polynôme et la fonction au point médian, et si cet écart est supérieur à un seuil de tolérance, on rajoute un point au milieu de l'intervalle.
Applications
- Étalonnage d'un appareil en métrologie : par la mesure de points connus (étalons), on ajuste les paramètres de la loi reliant l'intensité mesurée (en général, courant ou tension sortant du détecteur) à l'intensité du phénomène ; la loi sert donc à interpoler entre les points des étalons.
- Représentation graphique
- Éléments finis
- Usinage par interpolation
Voir aussi
- Interpolation lagrangienne
- Interpolation newtonienne
- Régression— Régression linéaire
- Extrapolation
- Approximation de fonction
- Simulation de profil
Lien externe
Interpolation methods, par Paul Bourke, décembre 1999
- Portail des mathématiques
Catégories : Interpolation numérique | Algorithme numérique
Wikimedia Foundation. 2010.