- Methode de Romberg
-
Méthode de Romberg
En analyse numérique, la méthode d'intégration de Romberg est une méthode récursive de calcul numérique d'intégrale, basée sur l'application du procédé d'extrapolation de Richardson à la méthode des trapèzes. Cette technique d'accélération permet d'améliorer l'ordre de convergence de la méthode des trapèzes, en appliquant cette dernière à des divisions dyadiques successives de l'intervalle d'étude et en en formant une combinaison judicieuse.
Sommaire
Principe
On souhaite calculer l'intégrale
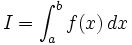 d'une fonction f, continue sur [a,b]. On subdivise alors [a,b] en n sous-intervalles identiques (n pair, n = 2p par exemple), du type [a + kh,a + (k + 1)h] pour k = 0,...,n − 1 et h = (b − a) / n. Sur cette grille régulière, est définie la méthode des trapèzes, notée T(h):
d'une fonction f, continue sur [a,b]. On subdivise alors [a,b] en n sous-intervalles identiques (n pair, n = 2p par exemple), du type [a + kh,a + (k + 1)h] pour k = 0,...,n − 1 et h = (b − a) / n. Sur cette grille régulière, est définie la méthode des trapèzes, notée T(h):où les pondérations ωk sont égales à 1 pour les points extrêmes, et à 2 pour les autres. Alors, l'erreur commise, notée
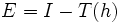 , vérifie
, vérifieCette relation exprime le fait que la méthode du trapèze présente une erreur proportionnelle à h2; on dit qu'elle est d'ordre O(h2).
Des manipulations algébriques fournissent une approximation de I d'ordre O(h4). Il suffit pour ce faire d'éliminer le terme en h2 dans le développement de l'erreur. On y parvient en considérant plutôt la quantité [4 T(h) – T(2h)]/3, qui n'est rien d'autre que la méthode de Simpson. Le même procédé peut être reconduit, afin d'annuler les termes en
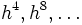 qui correspondent à des approximations de I de plus en plus précises.
qui correspondent à des approximations de I de plus en plus précises.Algorithme
Nous allons formaliser la technique précédente de réduction de l'erreur. On note par R(k,h) l'approximation de I à la k ème étape, avec une grille de pas h. On passe alors de l'étape k à l'étape k+1 en posant
On initialise l'algorithme avec la méthode du trapèze; autrement dit, R(0,h) = T(h). On montre par récurrence que l'approximation à la k ème étape, R(k,h), fournit une approximation de I qui est O(h2k + 2).L'algorithme peut être représenté sous la forme d'un tableau; afin de faciliter cette représentation, il est commode de remplacer le terme h = (b − a) / 2p par p directement. La première diagonale, notée R(k), correspond aux approximations successives, tandis que la première colonne représente la méthode du trapèze, la seconde la méthode de Simpson, etc. On se déplace à l'intérieur du tableau à l'aide de la formule de récurrence précédente. En pratique, pour obtenir une approximation de I au niveau ε > 0, on se fixe comme critère d'arrêt que la valeur absolue entre deux approximations successives est plus petite que ε. Ceci implique généralement que | R(k + 1) − I | < ε.
Exemple
A intégrer
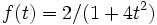 sur [-1,2]. On trouve
sur [-1,2]. On trouve 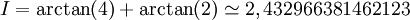 . La matrice de l'algorithme est
. La matrice de l'algorithme estk=0 1 2 3 4 p=0 0,7764705882 1 1,8882352941 2,2588235294 2 2,3510141988 2,5052738337 2,5217038540 3 2,4235526286 2,4477321053 2,4438959900 2,4426609446 4 2,4307735880 2,4331805744 2,4322104723 2,4320249879 2,4319832783 d'où l'on tire les approximations consécutives
k R(k) 0 0,77647058823529 1 2,25882352941176 2 2,52170385395538 3 2,44266094457555 4 2,43198327829659 Voir aussi
Lien externe
- Portail des mathématiques
Catégorie : Intégration numérique
Wikimedia Foundation. 2010.

![T(h) = \frac{h}{2} \left[\sum_{k=0}^{n} \omega_k f(a + k h)\right]](/pictures/frwiki/50/2b5b14039cd69a9ee45adf85c4e9da36.png)
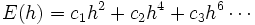
![R(k+1,h) = \frac{1}{4^{k+1}-1} \times \left[ 4^{k+1}R(k,h)-R(k,2h) \right]](/pictures/frwiki/97/a8dd3cbe0fc76dbce3d3cbbc49799bad.png)