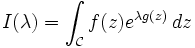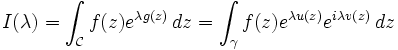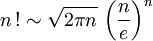Methode du point col

Methode du point col

Méthode du point col

En mathématiques, la méthode du point col (ou méthode de la descente rapide) permet d'évaluer le comportement asymptotique d'une intégrale complexe du type :

I(\lambda) = \int_\mathcal{C} f(z) e^{\lambda g(z)} \, dz\,

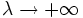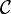lorsque \lambda\rightarrow +\infty. \mathcal{C} est un chemin d'intégration du plan complexe. f et g sont deux fonctions analytiques, et on note z = x + iy, g(z) = u(z) + iv(z) = u(x,y) + iv(x,y). Bien que reposant sur des concepts différents, la méthode du point col est généralement considérée comme l'extension de la méthode de la phase stationnaire aux intégrales complexes.

Sommaire

Idée générale

L'idée générale de la méthode consiste à déformer le chemin d'intégration grâce au théorème de Cauchy afin d'utiliser un chemin particulier γ, le chemin de descente rapide, sur lequel la partie imaginaire (c’est-à-dire la partie oscillante de l'exponentielle) de la fonction g est constante.

I(\lambda) = \int_\mathcal{C} f(z) e^{\lambda g(z)} \, dz = \int_\mathcal{\gamma} f(z)e^{\lambda u(z)} e^{i \lambda v(z)} \, dz

L'intégrale peut alors s'évaluer grâce à la méthode de Laplace. En notant zs le point col de la fonction g, c’est-à-dire le point pour lequel 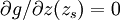\partial g/\partial z(z_s)=0, on a:

Un exemple classique : la formule de Stirling

On veut retrouver la formule de Stirling :

n\,!\sim \sqrt{2\pi n}\,\left({n \over e}\right)^n

En utilisant 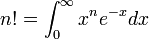n! = \int_0^{\infty}x^n e^{-x}dx, pour n grand ,

il apparaît un col dans la fonction exp [ n.ln(x)-x], au point x= n,
ce qui conduit à changer de variable : x = y + n .
Le crochet s'écrit alors [] = n.ln(n)-n -y.y/2n + f(y,n).

En étant prudent, le terme f(y,n) ne joue que "peu de rôle" et quand n tend vers l'infini le terme en y^2 donne, via l'intégrale gaussienne usuelle, sqrt(2.Pi.n). Un raffinement donne sqrt(2.Pi.(n+1/6)), mais...

Une application : la mécanique statistique

En mécanique statistique, on passe très souvent de l'équilibre "microcanonique" à l'équilibre "canonique". Le passage est, dans la limite thermodynamique des grands nombres de particules N, effectué par la méthode du col, dans une manière tout à fait similaire à l'exemple précédent. Schrödinger a été un grand promoteur de ce genre de calculs. Bien sûr, il l'a étendu à tous les calculs de transformée de Legendre, en particulier pour introduire le potentiel chimique.


Références

  • N. Bleistein, R.A. Handelsman, Asymptotic Expansions of Integrals, Dover, 1986 [1975].
  • L.B. Felsen, N. Marcuvitz, Radiation and Scattering of Waves, IEEE-Wiley, 1994 [1972], chap. 4.
  • E.T. Copson, Asymptotic Expansions, Cambridge University Press, 1965.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « M%C3%A9thode du point col ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Methode du point col de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Méthode Du Point Col — En mathématiques, la méthode du point col (ou méthode de la descente rapide) permet d évaluer le comportement asymptotique d une intégrale complexe du type : lorsque . est un chemin d intégration du plan complexe. f et g sont deux foncti …   Wikipédia en Français

  • Méthode du point col — En mathématiques, la méthode du point col (ou méthode de la descente rapide) permet d évaluer le comportement asymptotique d une intégrale complexe du type : lorsque . est un chemin d intégration du plan complexe. f et g sont deux fonctions… …   Wikipédia en Français

  • Point-col — Le point en rouge est un point col pour la fonction (ici la fonction z=x2−y2). En mathématiques, un point col (en anglais saddle point) pour une fonction f de plusieurs variables à valeurs dans …   Wikipédia en Français

  • Point col — Le point en rouge est le point du graphe de la fonction associé à son unique point selle (0,0). En mathématiques, un point selle (en anglais saddle point) d une fonction f définie sur un produit cartésien …   Wikipédia en Français

  • Point selle — Point col Le point en rouge est un point col pour la fonction (ici la fonction z=x2−y2). En mathématiques, un point col (en anglais saddle point) pour une fonction f de plusieurs variables à valeurs dans …   Wikipédia en Français

  • Methode de Laplace — Méthode de Laplace En mathématiques, la méthode de Laplace, due à Pierre Simon Laplace, est une méthode pour l évaluation numérique d intégrales de la forme : où f est une fonction deux fois dérivable, M est un grand nombre réel et les… …   Wikipédia en Français

  • Méthode De Laplace — En mathématiques, la méthode de Laplace, due à Pierre Simon Laplace, est une méthode pour l évaluation numérique d intégrales de la forme : où f est une fonction deux fois dérivable, M est un grand nombre réel et les bornes a et b peuvent… …   Wikipédia en Français

  • Méthode de laplace — En mathématiques, la méthode de Laplace, due à Pierre Simon Laplace, est une méthode pour l évaluation numérique d intégrales de la forme : où f est une fonction deux fois dérivable, M est un grand nombre réel et les bornes a et b peuvent… …   Wikipédia en Français

  • Méthode de Laplace — En mathématiques, la méthode de Laplace, due à Pierre Simon de Laplace, est une méthode pour l évaluation numérique d intégrales de la forme : où f est une fonction deux fois dérivable, M est un grand nombre réel et les bornes a et b peuvent …   Wikipédia en Français

  • Methode de la phase stationnaire — Méthode de la phase stationnaire En mathématiques, la méthode de la phase stationnaire permet d évaluer le comportement asymptotique d une intégrale du type : lorsque . (avec i2 = − 1) Sommaire 1 Idée générale …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”