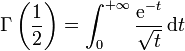Intégrale De Gauss

Intégrale de Gauss

Pour tout réel strictement positif $α$ , la fonction (paire) 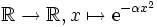$\R \to \R, x \mapsto \mathrm{e}^{-\alpha x^2}$ est intégrable sur $\R$ et :

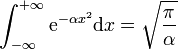$\int_{-\infty}^{+\infty} \mathrm{e}^{-\alpha x^2} \mathrm dx = \sqrt{\frac{\pi}{\alpha}}$ .

Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi normale. La valeur de cette intégrale fut donnée pour la première fois par Pierre-Simon Laplace.

Sommaire

1 Intégrabilité de la fonction
2 Calcul de l'intégrale de Gauss
- 2.1 Cas particulier α = 1
  - 2.1.1 Méthode classique
  - 2.1.2 Méthode utilisant une fonction définie par une intégrale
- 2.2 Cas général
3 Corollaire

Intégrabilité de la fonction

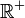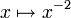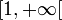Comme l'intégrande est pair, il suffit, pour montrer qu'il est intégrable sur $\R$ , de prouver qu'il est intégrable sur $\R^+$ . Cela résulte de ce qu'il est positif, continu, et négligeable à l'infini devant la fonction $x \mapsto x^{-2}$ , intégrable par exemple sur $[1,+\infty[$ .

Calcul de l'intégrale de Gauss

L'intégrande de l'intégrale de Gauss n'admet aucune primitive s'exprimant à l'aide des fonctions usuelles (exponentielle, etc.). Ceci oblige pour calculer cette intégrale à recourir à des méthodes plus ou moins « détournées », dont la plus classique et directe est celle qui utilise des intégrales doubles ; d'autres méthodes classiques existent dont une élémentaire, mais nettement plus longue, qui fait appel aux intégrales de Wallis et une autre qui utilise une fonction définie par une intégrale.

Cas particulier $α = 1$

Méthode classique

Démonstration

La méthode classique de calcul utilise une intégrale double qu'on exprime en coordonnées cartésiennes, puis en coordonnées polaires.

Soient

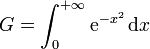$G = \int_0^{+\infty} \mathrm{e}^{-x^2}\, \mathrm dx$ et $H = \iint_{\R^+ \times \R^+} \mathrm{e}^{-(x^2 + y^2)}\, \mathrm dx\, \mathrm dy$ .

Compte tenu de ce que les variables $x$ et $y$ se séparent, le théorème de Fubini donne :

$H = \iint_{\R^+ \times \R^+} \mathrm{e}^{-x^2}\, \mathrm{e}^{-y^2}\, \mathrm dx\, \mathrm dy = \left(\int_0^{+\infty} \mathrm{e}^{-x^2}\, \mathrm dx\right) \left(\int_0^{+\infty} \mathrm{e}^{-y^2}\, \mathrm dy\right)= G^2$

On passe en coordonnées polaires en posant $x = r cosθ$ et $y = r sinθ$ ; les variables $r$ et $θ$ se séparent elles aussi :

$H = \iint_{\R^+ \times [0,\, \frac{\pi}{2}]} \mathrm{e}^{-r^2}\, r\, \mathrm dr\, \mathrm d\theta = \left(\int_0^{+\infty} \mathrm{e}^{-r^2}\, r\, \mathrm dr \right)\left(\int_0^{\frac{\pi}{2}}\, \mathrm d\theta\right) = \frac{1}{2} \cdot \frac{\pi}{2}$

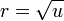car $\int_0^{+\infty} \mathrm{e}^{-r^2}\, r\, \mathrm dr = \frac{1}{2} \int_0^{+\infty} \mathrm{e}^{-u}\, \mathrm du = \frac{1}{2\,}$ (par le changement de variable $r = \sqrt u$ ).

On en déduit :

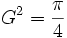$G^2 = \frac{\pi}{4}$ , d'où 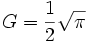$G = \frac{1}{2}\sqrt{\pi}$ puisque 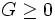$G \geq 0$ , et enfin : 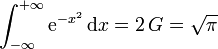$\int_{-\infty}^{+\infty} \mathrm{e}^{-x^2}\, \mathrm dx = 2\, G = \sqrt{\pi}$ par parité.

Méthode utilisant une fonction définie par une intégrale

Article détaillé : Intégrale paramétrique.

Cette méthode plus élémentaire n'utilise que des résultats sur les intégrales simples (à une seule variable) usuelles (sur un intervalle fermé borné).

On pose, pour tout x réel, 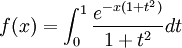$f(x)=\int_{0}^{1}{\frac{e^{-x(1+t^2)}}{1+t^2}dt}$ . On montre d'abord que $f$ est dérivable sur $\mathbb{R}$ et que sa dérivée est donnée, pour tout x réel, par : 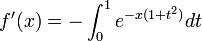$f'(x)=-\int_{0}^{1}{e^{-x(1+t^2)}dt}$ .

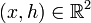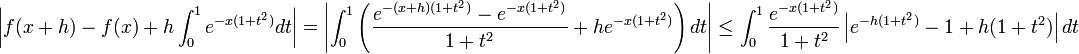
On a, pour tout $(x,h)\in\mathbb{R}^2$ , $\left| f(x+h)-f(x)+h\int_{0}^{1}{e^{-x(1+t^2)}dt}\right|=\left| \int_{0}^{1}{\left( \frac{e^{-(x+h)(1+t^2)}-e^{-x(1+t^2)}}{1+t^2} + he^{-x(1+t^2)} \right) dt}\right| \leq \int_{0}^{1}{\frac{e^{-x(1+t^2)}}{1+t^2}\left| e^{-h(1+t^2)}-1+h(1+t^2) \right| dt}$

Or, en appliquant l'inégalité de Taylor-Lagrange à l'ordre 2 à la fonction exponentielle entre $0$ et $- h (1 + t 2)$ , on obtient pour tout 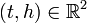$(t,h)\in\mathbb{R}^2$ la majoration :

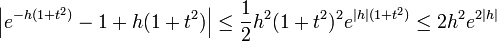$\left| e^{-h(1+t^2)}-1+h(1+t^2) \right| \leq \frac{(-h(1+t^2))^2}{2!}M$ où $M$ est un majorant de la fonction exponentielle entre $0$ et $- h (1 + t 2)$ , par exemple $M=e^{|h|(1+t^2)}$ , donc pour $t\in[0,1]$ on obtient : $\left| e^{-h(1+t^2)}-1+h(1+t^2) \right| \leq \frac{1}{2}h^2(1+t^2)^2e^{|h|(1+t^2)} \leq 2h^2e^{2|h|}$ .

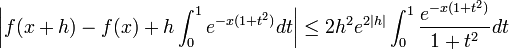On en déduit dans l'inégalité d'origine : $\left| f(x+h)-f(x)+h\int_{0}^{1}{e^{-x(1+t^2)}dt}\right| \leq 2h^2e^{2|h|}\int_{0}^{1}{\frac{e^{-x(1+t^2)}}{1+t^2}dt}$ .

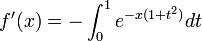En divisant par $| h |$ pour $h$ non nul, puis en faisant tendre $h$ vers $0$ , on obtient par encadrement, pour tout x réel, la dérivabilité de f en x et la relation : $f'(x)=-\int_{0}^{1}{e^{-x(1+t^2)}dt}$ .

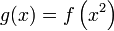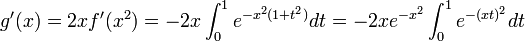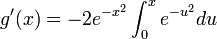On considère maintenant la fonction $g$ définie, pour tout x réel, par $g(x)=f\left(x^2\right)$ . D'après ce qui précède, et par composition, g est dérivable sur $\mathbb{R}$ , et pour tout x réel, $g'(x)=2xf'(x^2)=-2x\int_{0}^{1}{e^{-x^2(1+t^2)}dt}=-2xe^{-x^2}\int_{0}^{1}{e^{-(xt)^2}dt}$ , d'où par le changement de variable $u = x t$ , $g'(x)=-2e^{-x^2}\int_{0}^{x}{e^{-u^2}du}$ .

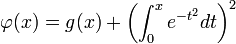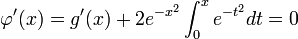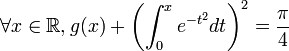On montre alors que la fonction $\varphi (x)=g(x)+{\left( \int_{0}^{x}{e^{-t^2}dt} \right)}^2$ est constante sur $\mathbb{R}$ . En effet, pour tout x réel, $\varphi '(x)=g'(x)+2e^{-x^2}\int_{0}^{x}{e^{-t^2}dt}=0$ , et comme $\varphi (0)=g(0)=f(0)=\int_{0}^{1}{\frac{1}{1+t^2}dt}=\left[\mathrm{Arctan}(t)\right ]_{0}^{1}=\frac{\pi}{4}$ , on en déduit l'égalité : $\forall x \in \mathbb{R}, g(x)+{\left( \int_{0}^{x}{e^{-t^2}dt} \right)}^2=\frac{\pi}{4}$ . Il ne reste plus qu'à étudier la limite de cette expression lorsque $x$ tend vers $+\infty$ .

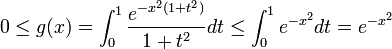On a : $0 \leq g(x) = \int_{0}^{1}{\frac{e^{-x^2(1+t^2)}}{1+t^2}dt} \leq \int_{0}^{1}{e^{-x^2}dt} = e^{-x^2}$ , donc par encadrement 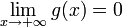$\lim_{x \to +\infty}{g(x)} = 0$ , d'où le résultat recherché : $\int_{0}^{+\infty}{e^{-t^2}dt=\frac{\sqrt{\pi}}{2}}$ .

Cas général

En effectuant dans l'intégrale de Gauss le changement de variable défini par $x = \tfrac{t}{\sqrt{\alpha}}$ , on obtient :

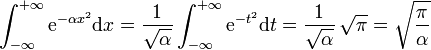$\int_{-\infty}^{+\infty} \mathrm{e}^{-\alpha x^2} \mathrm dx =\frac{1}{\sqrt{\alpha}}\int_{-\infty}^{+\infty} \mathrm{e}^{-t^2} \mathrm dt = \frac{1}{\sqrt{\alpha}}\, \sqrt{\pi} = \sqrt{\frac{\pi}{\alpha}}$ .

Corollaire

Le réel

$\Gamma\left(\frac{1}{2}\right) = \int_0^{+\infty} \frac{\mathrm{e}^{-t}}{\sqrt{t}}\, \mathrm dt$

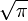(une valeur de la fonction Gamma d'Euler) est égal à $\sqrt{\pi}$ .

Démonstration

En effet, effectuant dans l'intégrale ci-dessus le changement de variable $t = x 2$ , où $x > 0$ , on obtient :

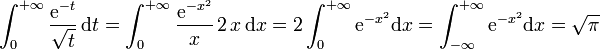$\int_0^{+\infty} \frac{\mathrm{e}^{-t}}{\sqrt{t}}\, \mathrm dt = \int_0^{+\infty} \frac{\mathrm{e}^{-x^2}}{x}\, 2\, x\, \mathrm dx = 2 \int_{0}^{+\infty} \mathrm{e}^{-x^2} \mathrm dx = \int_{-\infty}^{+\infty} \mathrm{e}^{-x^2} \mathrm dx = \sqrt{\pi}$ .

Portail des mathématiques

Ce document provient de « Int%C3%A9grale de Gauss ».

Catégories : Intégrale | Carl Friedrich Gauss

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Intégrale De Gauss de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Integrale de Gauss — Intégrale de Gauss Pour tout réel strictement positif α, la fonction (paire) est intégrable sur et : . Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi … Wikipédia en Français
Intégrale de gauss — Pour tout réel strictement positif α, la fonction (paire) est intégrable sur et : . Cette intégrale est appelée intégrale de Gauss. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi normale. La valeur … Wikipédia en Français
Intégrale de Gauss — La surface comprise entre la courbe d équation y = exp(−x2) et l axe des abscisses vaut √π. En mathématiques, une intégrale de Gauss est l intégrale d une fonction gaussienne sur l ensemble des réels. Sa valeur est reliée à la constante π par la… … Wikipédia en Français
Intégrale à paramètre — Intégrale paramétrique En mathématiques, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction définie à partir de l intégration d une fonction de plusieurs variables sur un ensemble fixe par rapport à une partie… … Wikipédia en Français
Intégrale à paramètres — Intégrale paramétrique En mathématiques, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction définie à partir de l intégration d une fonction de plusieurs variables sur un ensemble fixe par rapport à une partie… … Wikipédia en Français
Integrale impropre — Intégrale impropre En mathématiques, l intégrale impropre désigne une extension de l intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des… … Wikipédia en Français
Intégrale Impropre — En mathématiques, l intégrale impropre désigne une extension de l intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des véritables intégrales ou… … Wikipédia en Français
Intégrale généralisée — Intégrale impropre En mathématiques, l intégrale impropre désigne une extension de l intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des… … Wikipédia en Français
Integrale de Fresnel — Intégrale de Fresnel Pour les articles homonymes, voir Fresnel. L intégrale de Fresnel est une intégrale impropre introduite par le physicien français Augustin Fresnel. Formule de Fresnel … Wikipédia en Français
Intégrale De Fresnel — Pour les articles homonymes, voir Fresnel. L intégrale de Fresnel est une intégrale impropre introduite par le physicien français Augustin Fresnel. Formule de Fresnel … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Intégrale De Gauss