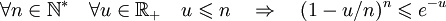Integrales de Wallis

Intégrales de Wallis

En analyse, les intégrales de Wallis constituent une famille d'intégrales introduites par John Wallis.

Sommaire

1 Définition, premières propriétés
2 Relation de récurrence, calcul des intégrales de Wallis
3 Un équivalent de la suite des intégrales de Wallis
4 Application à la formule de Stirling
5 Application au calcul de l'intégrale de Gauss
6 Nota

Définition, premières propriétés

On appelle habituellement intégrales de Wallis les termes de la suite réelle 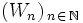$(W_n)_{\,n\, \in\, \mathbb{N}\,}$ définie par :

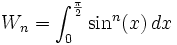$W_n = \int_0^{\frac{\pi}{2}} \sin^n(x)\,dx$ , ou de façon équivalente (par le changement de variable: $x = \frac{\pi}{2} - t$ )

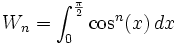
$W_n = \int_0^{\frac{\pi}{2}} \cos^n(x)\,dx$

En particulier, les deux premiers termes de cette suite sont :

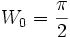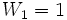
$\quad W_0=\frac{\pi}{2}\qquad \,$ et $\quad W_1=1\,$

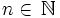La suite $\ (W_n)$ est décroissante, à termes strictement positifs. En effet, pour tout $n \in\, \mathbb{N}$ :

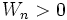$\ W_n > 0$ : c'est l'intégrale d'une fonction continue, positive, et non identiquement nulle sur l'intervalle d'intégration
$W_{n} - W_{n + 1}= \int_0^{\frac{\pi}{2}} \sin^{n}(x)\,dx - \int_0^{\frac{\pi}{2}} \sin^{n + 1}(x)\,dx = \int_0^{\frac{\pi}{2}} \sin^{n}(x)\, [1 - \sin(x)]\,dx \geqslant 0$

(par linéarité de l'intégrale et parce que la dernière intégrale est celle d'une fonction positive sur l'intervalle d'intégration)

Nota : décroissante et minorée (par 0), la suite $\ (W_n)$ converge, et sa limite est positive ou nulle ; en fait, elle est nulle, comme cela résulte de l'équivalent obtenu plus loin.

Relation de récurrence, calcul des intégrales de Wallis

Une intégration par parties va permettre d'établir une relation de récurrence intéressante :

En remarquant que pour tout réel $x$ , $\quad \sin^2(x) = 1-\cos^2(x)$ , on a pour tout entier naturel n≥2 :

$\int_0^{\frac{\pi}{2}} \sin^{n}(x)\,dx = \int_0^{\frac{\pi}{2}} \sin^{n-2}(x) \left[1-\cos^2(x)\right]\,dx$

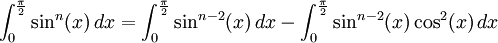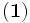$\int_0^{\frac{\pi}{2}} \sin^{n}(x)\,dx = \int_0^{\frac{\pi}{2}} \sin^{n-2}(x)\,dx - \int_0^{\frac{\pi}{2}} \sin^{n-2}(x) \cos^2(x)\,dx$ (relation $\mathbf{(1)}$ )

On intègre alors par parties la seconde intégrale du second membre, en posant:

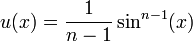
$u'(x) = cos(x)sin n - 2 (x)$ dont la primitive est $u(x) = \frac{1}{n-1} \sin^{n-1}(x)$
$v (x) = cos(x)$ de dérivée $v'(x) = - sin(x)$

$\int_0^{\frac{\pi}{2}} \sin^{n-2}(x) \cos^2(x)\,dx = \left[ \frac{1}{n-1} \sin^{n-1}(x) \cos(x)\right]_0^{\frac{\pi}{2}} + \int_0^{\frac{\pi}{2}} \ \frac{1}{n-1} \sin^{n-1}(x) \sin(x)\,dx = 0 + {1\over {n-1}}\,W_{n}$

En reportant dans $\mathbf{(1)}$ , on obtient alors:

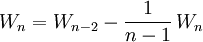
$W_n=W_{n-2} - {1\over {n-1}}\,W_{n}$

d'où:

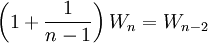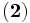$\qquad \left(1+ \frac{1}{n-1}\right)W_n=W_{n-2}$ (relation $\mathbf{(2)}$ )

Ceci se traduit par la relation bien connue :

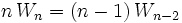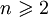$n\,W_n = (n-1)\,W_{n-2}\qquad \,$ , valable pour $n \geqslant 2\qquad \,$ .

On a là une relation de récurrence donnant $W n$ en fonction de $W n - 2$ , c'est-à-dire le n-ième terme de la suite en fonction du (n-2)-ième. De cette relation et des valeurs de $W 0$ et $W 1$ , on tire une expression des termes de la suite, selon la parité de leur rang. Ainsi :

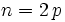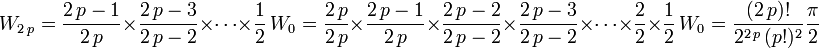
pour $\quad n=2\,p$ , $\quad W_{2\,p}=\frac{2\,p-1}{2\,p}\times\frac{2\,p-3}{2\,p-2}\times\cdots\times\frac{1}{2}\,W_0=\frac{2\,p}{2\,p}\times\frac{2\,p-1}{2\,p}\times\frac{2\,p-2}{2\,p-2}\times\frac{2\,p-3}{2\,p-2}\times\cdots\times\frac{2}{2}\times\frac{1}{2}\,W_0 = \frac{(2\,p)!}{2^{2\,p}\, (p!)^2} \frac{\pi}{2}$
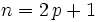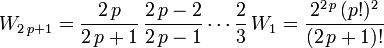
pour $\quad n=2\,p+1$ , $\quad W_{2\,p+1}=\frac{2\,p}{2\,p+1}\,\frac{2\,p-2}{2\,p-1}\cdots\frac{2}{3}\,W_1=\frac{2^{2\,p}\, (p!)^2}{(2\,p +1)!}~$

On remarque que les termes de rang pair sont irrationnels, tandis que ceux de rang impair sont rationnels.

Un équivalent de la suite des intégrales de Wallis

De la formule de récurrence précédente 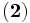$\mathbf{(2)}$ , on déduit d'abord que :

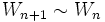$\ W_{n + 1} \sim W_n$ (équivalence de deux suites).

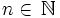En effet, pour tout $n \in\, \mathbb{N}$ :

$\ W_{n + 2} \leqslant W_{n + 1} \leqslant W_n$ (la suite étant décroissante) donc :

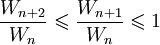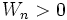$\frac{W_{n + 2}}{W_n} \leqslant \frac{W_{n + 1}}{W_n} \leqslant 1$ (puisque $\ W_n > 0$ ), ce qui s'écrit :

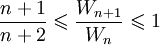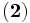$\frac{n + 1}{n + 2} \leqslant \frac{W_{n + 1}}{W_n} \leqslant 1$ (d'après la relation $\mathbf{(2)}$ ).

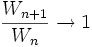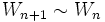Par encadrement, on conclut que $\frac{W_{n + 1}}{W_n} \to 1$ , soit $\ W_{n + 1} \sim W_n$ .

Puis on établit l'équivalence suivante :

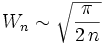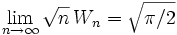$W_n \sim \sqrt{\frac{\pi}{2\, n}}\quad$ ( soit encore $\quad\lim_{n \rightarrow \infty} \sqrt n\,W_n=\sqrt{\pi /2}\quad$ ).

Démonstration

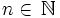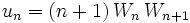Pour tout $n \in\, \mathbb{N}$ , posons $u_n = (n + 1)\, W_n\, W_{n + 1}$ .

Alors, 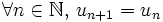$\forall n\in \N,\, u_{n + 1} = u_n$ d'après la relation 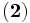$\mathbf{(2)}$ : la suite 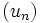$\ (u_n)$ est donc constante.

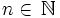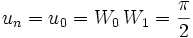On en déduit que pour tout $n \in\, \mathbb{N}$ , $u_n = u_0 = W_0\, W_1 = \frac{\pi}{2}$ .

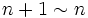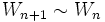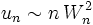Par ailleurs, puisque $\ n + 1 \sim n$ et $\ W_{n + 1} \sim W_n$ , on a $\ u_n \sim n\, W_n^2$ , par produit d'équivalents.

Ainsi, 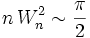$\ n\, W_n^2 \sim \frac{\pi}{2}$ , d'où découle (puisque 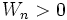$\ W_n > 0$ ) l'équivalence annoncée.

Application à la formule de Stirling

On suppose connue l'équivalence suivante (établie dans l'article sur la formule de Stirling):

$\ n\,! \sim C\, \sqrt{n}\left(\frac{n}{\mathrm{e}}\right)^n$ , où $\ C \in \R^*$ .

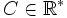On se propose maintenant de déterminer la constante 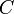$\ C$ à l'aide d'équivalents de $W_{2\, p}$ .

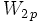Du paragraphe précédent résulte l'équivalence :

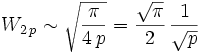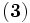$W_{2\, p} \sim \sqrt{\frac{\pi}{4\, p}} = \frac{\sqrt{\pi}}{2}\, \frac{1}{\sqrt{p}}$ (relation $\mathbf{(3)}$ )

Par ailleurs, en utilisant l'équivalent de la factorielle donné supra :

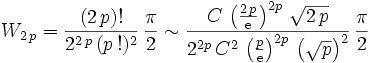$W_{2\,p}=\frac{(2\,p)!}{2^{2\,p}\, (p\,!)^2}\, \frac{\pi}{2} \sim \frac{C\, \left(\frac{2\, p}{\mathrm{e}}\right)^{2p}\, \sqrt{2\, p}}{2^{2p}\, C^2\, \left(\frac{p}{\mathrm{e}}\right)^{2p}\, \left(\sqrt{p}\right)^2}\, \frac{\pi}{2}$ , soit :

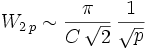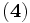$W_{2\,p} \sim \frac{\pi}{C\, \sqrt{2}}\, \frac{1}{\sqrt{p}}$ (relation $\mathbf{(4)}$ )

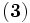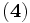Des équivalences $\mathbf{(3)}$ et $\mathbf{(4)}$ , on déduit par transitivité :

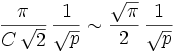$\frac{\pi}{C\, \sqrt{2}}\, \frac{1}{\sqrt{p}} \sim \frac{\sqrt{\pi}}{2}\, \frac{1}{\sqrt{p}}$ , d'où :

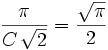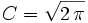$\frac{\pi}{C\, \sqrt{2}} = \frac{\sqrt{\pi}}{2}$ , et enfin $C = \sqrt{2\, \pi}$ .

On a ainsi établi la formule de Stirling:

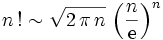$\ n\,! \sim \sqrt{2\, \pi\, n}\, \left(\frac{n}{\mathrm{e}}\right)^n$ .

Application au calcul de l'intégrale de Gauss

On peut aisément utiliser les intégrales de Wallis pour calculer l'intégrale de Gauss.

Vérifions d'abord les inégalités suivantes:

$\forall n\in \mathbb N^* \quad \forall u\in\mathbb R_+ \quad u\leqslant n\quad\Rightarrow\quad (1-u/n)^n\leqslant e^{-u}$
$\forall n\in \mathbb N^* \quad \forall u \in\mathbb R_+ \qquad e^{-u} \leqslant (1+u/n)^{-n}$

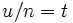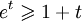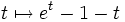En effet en posant $\quad u/n=t$ la première inégalité (pour laquelle $t \in [0,1]$ ) équivaut à $1-t\leqslant e^{-t}$ . Quant à la seconde elle s'écrit $e^{-t}\leqslant (1+t)^{-1}$ , ce qui revient à $e^t\geqslant 1+t$ . Ces 2 inégalités sont des conséquences immédiates de la convexité de la fonction exponentielle (ou si l'on préfère de l'étude de la fonction $t \mapsto e^t -1 -t$ ).

Posant alors $u = x 2$ et utilisant les propriété élémentaires des intégrales impropres (la convergence des intégrales est immédiate) on obtient l'encadrement:

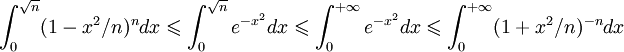$\int_0^{\sqrt n}(1-x^2/n)^n dx \leqslant \int_0^{\sqrt n} e^{-x^2} dx \leqslant \int_0^{+\infty} e^{-x^2} dx \leqslant \int_0^{+\infty} (1+x^2/n)^{-n} dx$ .

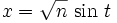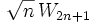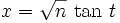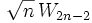Or les intégrales d'encadrement se ramènent facilement à des intégrales de Wallis. Pour celle de gauche il suffit de poser $x=\sqrt n\, \sin\,t$ (t variant de 0 à $π / 2$ ) et elle s'écrit $\sqrt n \,W_{2n+1}$ . Quant à celle de droite, on peut poser $x=\sqrt n\, \tan\, t$ (t variant de $0$ à $π / 2$ ) qui donne $\sqrt n \,W_{2n-2}$ .

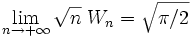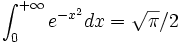Comme on a vu que $\lim_{n\rightarrow +\infty} \sqrt n\;W_n=\sqrt{\pi /2}$ , on en déduit que $\int_0^{+\infty} e^{-x^2} dx = \sqrt{\pi} /2$ .

Remarque : Il existe bien d'autres méthodes de calcul de l'intégrale de Gauss, dont une méthode bien plus directe.

Nota

Les mêmes propriétés conduisent au produit de Wallis, qui exprime 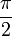$\frac{\pi}{2}\,$ (voir π) sous forme d'un produit infini.

Portail des mathématiques

Ce document provient de « Int%C3%A9grales de Wallis ».

Catégories : Analyse | Intégrale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Integrales de Wallis de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Intégrales De Wallis — En analyse, les intégrales de Wallis constituent une famille d intégrales introduites par John Wallis. Sommaire 1 Définition, premières propriétés 2 Relation de récurrence, calcul des intégrales de Wallis … Wikipédia en Français
Intégrales de wallis — En analyse, les intégrales de Wallis constituent une famille d intégrales introduites par John Wallis. Sommaire 1 Définition, premières propriétés 2 Relation de récurrence, calcul des intégrales de Wallis … Wikipédia en Français
Intégrales de Wallis — En mathématiques, et plus précisément en analyse, les intégrales de Wallis constituent une famille d intégrales introduites par John Wallis. Sommaire 1 Définition, premières propriétés 2 Relation de récurrence, calcul des intégrales de Wallis … Wikipédia en Français
Wallis — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Géographie Wallis, nom allemand du canton suisse de Valais Wallis, une des deux îles de la collectivité d outre mer française de Wallis et Futuna Wallis,… … Wikipédia en Français
Intégrale de Wallis — Intégrales de Wallis En analyse, les intégrales de Wallis constituent une famille d intégrales introduites par John Wallis. Sommaire 1 Définition, premières propriétés 2 Relation de récurrence, calcul des intégrales de Wallis … Wikipédia en Français
Integral de Wallis — Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a… … Wikipedia Español
John Wallis — Pour les articles homonymes, voir Wallis. John Wallis John Wallis, né le 23 novembre 1616 à Ashford … Wikipédia en Français
Table d'integrales — Table d intégrales Intégrales définies On appelle intégrale définie dans l intervalle [a,b] lorsque est une primitive quelconque de et que et … Wikipédia en Français
Table d'intégrales — Sommaire 1 Intégrales définies 1.1 Voyez aussi 1.2 Articles connexes 1.3 Liens externes Intégrales dé … Wikipédia en Français
John Wallis : Les Applications Cliniques De La Phonétique Et L'éducation Des Sourds — John Wallis Pour les articles homonymes, voir Wallis. John Wallis John Wallis, né le 23 novembre … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Integrales de Wallis

Intégrales de Wallis

Sommaire

Définition, premières propriétés

Relation de récurrence, calcul des intégrales de Wallis

Un équivalent de la suite des intégrales de Wallis

Application à la formule de Stirling

Application au calcul de l'intégrale de Gauss

Nota

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Integrales de Wallis

Intégrales de Wallis

Sommaire

Définition, premières propriétés

Relation de récurrence, calcul des intégrales de Wallis

Un équivalent de la suite des intégrales de Wallis

Application à la formule de Stirling

Application au calcul de l'intégrale de Gauss

Nota

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link