Intégrale De Dirichlet

Intégrale de Dirichlet

L' intégrale de Dirichlet est l'intégrale de la fonction sinus cardinal sur la demi-droite des réels positifs

$\int_0^{+\infty}\frac{\sin(x)}{x}\,dx = \frac{\pi}{2}$

Il s'agit d'une intégrale impropre semi-convergente, c'est-à-dire que la fonction n'est pas intégrable au sens généralisé de Riemann, mais 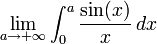$\lim_{a \to +\infty} \int_0^{a}\frac{\sin(x)}{x}\,dx$ existe.

Preuve

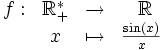
On considère la fonction : $\begin{matrix}f: & \mathbb{R}_{+}^{*}& \rightarrow & \mathbb{R} \\ & x & \mapsto & \frac{\sin(x)}{x}\ \\\end{matrix}$

On a 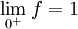$\lim_{0^{+}} f = 1\$ , donc $f$ est prolongeable par continuité en 0.

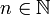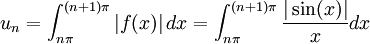Montrons que cette fonction n'est pas intégrable : on considère, pour tout $n \in \mathbb{N}$ , la suite : $u_n = \int_{n \pi} ^{(n+1) \pi} |f(x)|\,dx = \int_{n \pi} ^{(n+1) \pi} \frac{| \sin(x) |}{x}dx$ .

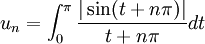Le changement de variables $t = x - n π$ donne $u_n = \int_{0} ^{\pi} \frac{| \sin(t + n \pi) |}{t + n \pi}dt$ .

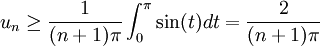On peut alors écrire : $u_n \geq \frac{1}{(n+1)\pi}\int_{0} ^{\pi} \sin(t)dt = \frac{2}{(n+1) \pi}$ .

On en déduit : 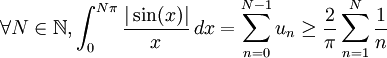$\forall N \in \mathbb{N} , \int_0^{N \pi}\frac{| \sin(x)|}{x}\,dx = \sum_{n=0} ^{N-1} u_n \geq \frac{2}{\pi} \sum_{n=1} ^N \frac{1}{n}$ , or cette série est la série harmonique, qui diverge.

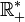La fonction $f$ n'est donc pas intégrable sur $\mathbb{R}_{+}^{*}$ .

Montrons maintenant que 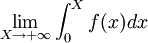$\lim_{X \to +\infty} \int_0^{X} f(x)dx$ existe.

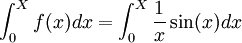On a $\int_0^{X} f(x)dx = \int_0^{X} \frac{1}{x} \sin(x)dx$ .

Une intégration par parties, avec 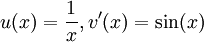$u(x) = \frac{1}{x} , v'(x)= \sin(x)$ , puis en prenant 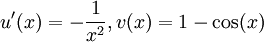$u'(x) = - \frac{1}{x^2} , v(x)=1- \cos(x)$ , permet d'écrire, abusivement : $\int_0^{X} f(x)dx = \left[ \frac{1- \cos(x)}{x} \right] _{0}^{X} + \int_{0}^{X} \frac{1- \cos(x)}{x^2} dx$ .

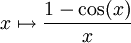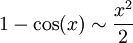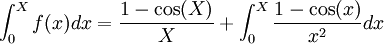L'abus vient du fait que $x \mapsto \frac{1- \cos(x)}{x}$ n'est pas défini en 0. Cependant, comme on a en 0 : $1- \cos(x) \sim \frac{x^2}{2}$ , on écrit : $\int_0^{X} f(x)dx = \frac{1- \cos(X)}{X} + \int_{0}^{X} \frac{1- \cos(x)}{x^2} dx$ .

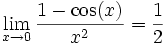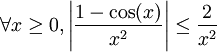De plus, comme on a $\lim_{x \to 0} \frac{1- \cos(x)}{x^2} = \frac{1}{2}$ et $\forall x \geq 0 , \left| \frac{1- \cos(x)}{x^2} \right| \leq \frac{2}{x^2}$ , on en déduit donc que 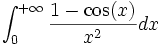$\int_{0}^{+ \infty} \frac{1- \cos(x)}{x^2} dx$ converge.

Avec 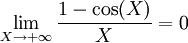$\lim_{X \to +\infty} \frac{1- \cos(X)}{X}=0$ , on en conclut que 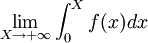$\lim_{X \to +\infty} \int_0^{X} f(x)dx$ existe.

Calcul de l'intégrale de Dirichlet

Avec des suites

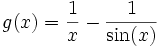Posons, pour $x \in \left] 0 ; \frac{\pi}{2} \right]$ , la fonction $g(x)= \frac{1}{x}- \frac{1}{\sin(x)}$ .

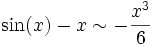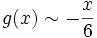Comme on a en 0 : $sin(x)˜ x$ et $\sin(x) - x \sim -\frac{x^3}{6}$ , on a donc, toujours en 0 : $g(x) \sim -\frac{x}{6}$ .

La fonction g est donc continue sur sur $\left] 0 ; \frac{\pi}{2} \right]$ , et prolongeable par continuité en 0.

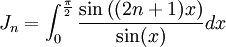On considère maintenant la suite d'intégrales $J_n = \int_{0} ^{\frac{\pi}{2}} \frac{\sin \left ( ( 2n+1) x \right)}{\sin(x)} dx$ .

Comme 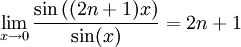$\lim_{x \to 0} \frac{\sin \left((2n+1)x \right)}{\sin(x)}=2n+1$ , la suite 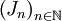$\left( J_n \right)_{n \in \mathbb{N}}$ est bien définie.

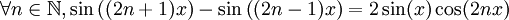De plus, remarquons que $\forall n \in \mathbb{N} , \sin \left((2n+1) x \right) - \sin \left((2n-1) x \right) = 2 \sin(x) \cos(2nx)$ .

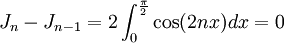On en tire alors $J_n - J_{n-1} = 2 \int_{0} ^{\frac{\pi}{2}} \cos (2nx) dx = 0$ .

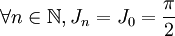La suite $J n$ est donc constante, et $\forall n \in \mathbb{N} , J_n = J_0 = \frac{\pi}{2}$ .

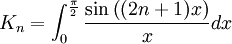On considère maintenant la suite d'intégrales $K_n = \int_{0} ^{\frac{\pi}{2}} \frac{\sin \left ( ( 2n+1) x \right)}{x} dx$ .

Comme 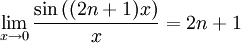$\lim_{x \to 0} \frac{\sin \left((2n+1)x \right)}{x}=2n+1$ , la suite 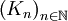$\left( K_n \right)_{n \in \mathbb{N}}$ est bien définie.

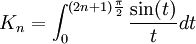Le changement de variables $t = (2 n + 1) x$ donne $K_n = \int_{0} ^{(2n+1) \frac{\pi}{2}} \frac{\sin (t)}{t} dt$ .

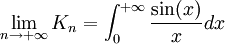On en déduit alors $\lim_{n \to +\infty} K_n = \int_{0} ^{+\infty} \frac{\sin(x)}{x} dx$ .

On a : $\forall n \in \mathbb{N} , K_n - J_n = \int_{0} ^{\frac{\pi}{2}} g(x) \sin \left((2n+1) x \right) dx$ .

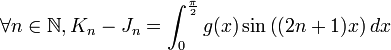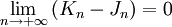On a vu que la fonction g est continue sur $\left] 0 ; \frac{\pi}{2} \right]$ , donc par le lemme de Riemann-Lebesgue, $\lim_{n \to +\infty} \left(K_n - J_n \right) = 0$ .

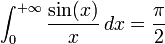On en conclut : $\int_0^{+\infty}\frac{\sin(x)}{x}\,dx = \frac{\pi}{2}$ .

Avec le théorème des résidus

En remarquant que 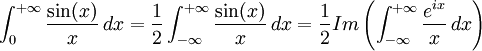$\int_0^{+\infty}\frac{\sin(x)}{x}\,dx = \frac{1}{2} \int_{-\infty} ^{+\infty}\frac{\sin(x)}{x}\,dx =\frac{1}{2} Im \left(\int_{-\infty} ^{+\infty}\frac{e^{ix}}{x}\,dx \right )$ , et en considérant la fonction complexe 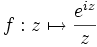$f : z \mapsto \frac{e^{iz}}{z}$ , le théorème des résidus donne le résultat voulu. Il faut faire attention, au niveau du contour, à faire un petit détour autour de zéro car la fonction 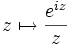$z \mapsto \frac{e^{iz}}{z}$ y possède un pôle.
Plus précisément, considérons le contour défini comme suit : pour deux réels $R > ε > 0$ , on choisit le demi-cercle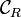 $\mathcal{C}_{R}$ de centre $O$ , de rayon $R$ situé dans le demi-plan supérieur, le demi-cercle 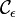$\mathcal{C}_{\epsilon}$ de centre $O$ , de rayon $ε$ situé dans le demi-plan inférieur et on les relie par deux segments $I$ et $J$ . Cette courbe délimite un domaine borné du plan contenant l'origine.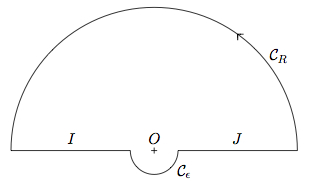

Contour Dirichlet.jpg

La fonction $f$ admet en $O$ un unique pôle de muliplicité $1$ . La formule des résidus donne alors

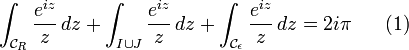$\int_{\mathcal{C}_{R}}\frac{e^{iz}}{z}\,dz+\int_{I\cup J}\frac{e^{iz}}{z}\,dz+\int_{\mathcal{C}_{\epsilon}}\frac{e^{iz}}{z}\,dz=2i\pi\;\;\;\;\;\;(1)$ .

Le cercle 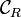$\mathcal{C}_{R}$ se paramètre par 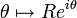$\theta\mapsto Re^{i\theta}$ , pour $θ$ variant entre $0$ et $π$ . On a alors 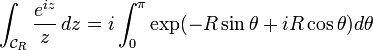$\int_{\mathcal{C}_{R}}\frac{e^{iz}}{z}\,dz=i\int_{0}^{\pi}\exp(-R\sin\theta+iR\cos\theta)d\theta$ . Il s'ensuit que 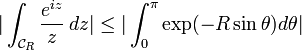$| \int_{\mathcal{C}_{R}}\frac{e^{iz}}{z}\,dz |\leq | \int_{0}^{\pi}\exp(-R\sin\theta)d\theta |$ . Cette dernière intégrale est une fonction décroissante de $R$ ; elle admet donc une limite en $+\infty$ . 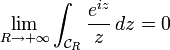En appliquant par exemple le théorème de convergence dominée, il vient alors $\lim\limits_{R\to+\infty}\int_{\mathcal{C}_{R}}\frac{e^{iz}}{z}\,dz=0$ .
De même, le cercle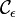 $\mathcal{C}_{\epsilon}$ se paramètre par 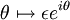$\theta\mapsto \epsilon e^{i\theta}$ , pour $θ$ variant entre $π$ et $2π$ . On a alors $\int_{\mathcal{C}_{\epsilon}}\frac{e^{iz}}{z}\,dz=i\int_{0}^{\pi}\exp(-\epsilon\sin\theta+i\epsilon\cos\theta)d\theta\xrightarrow[\epsilon\to 0]{}i\pi$ .
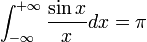En prenant la partie imaginaire de l'équation $(1)$ puis en faisant tendre $R$ vers $+\infty$ et $ε$ vers $0$ , il vient alors $\int_{-\infty}^{+\infty}\frac{\sin x}{x}dx=\pi$ .
On peut aller un peu plus vite en considérant la fonction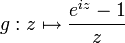 $g : z\mapsto\frac{e^{iz}-1}{z}$ qui se prolonge en une fonction holomorphe en $0$ . On intègre alors sur le contour constitué du cercle 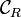$\mathcal{C}_{R}$ et de l'intervalle $[ - R, R]$ . Par le théorème de Cauchy, cette intégrale vaut $0$ . Mais d'autre part $\int_{\mathcal{C}_{R}}\frac{e^{iz}-1}{z}\,dz=\int_{\mathcal{C}_{R}}\frac{e^{iz}}{z}\,dz-\int_{\mathcal{C}_{R}}\frac{dz}{z}=\int_{\mathcal{C}_{R}}\frac{e^{iz}}{z}\,dz-i\pi\xrightarrow[R\to+\infty]{}-i\pi$ . 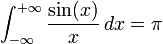En prenant la partie imaginaire et en faisant tendre $R$ vers $+\infty$ , il vient à nouveau $\int_{-\infty}^{+\infty}\frac{\sin(x)}{x}\,dx=\pi$ .

Avec une transformée de Laplace

Grâce à la transformée de Laplace, on peut calculer la valeur de l'intégrale de Dirichlet.

En effet, admettons que si $\mathcal{L}^{-1}[F(p)]=\operatorname{f}(x)$ , alors $\mathcal{L}^{-1}\left[\int_p^{+\infty}F(u)du\right]=\frac{\operatorname{f}(x)}{x}$

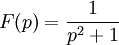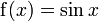
Choisissons $F(p)=\frac{1}{p^2+1}$ et $\operatorname{f}(x)=\sin x$

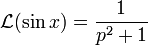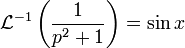
On sait de plus que $\mathcal{L}(\sin x)=\frac{1}{p^2+1}$ d'où $\mathcal{L}^{-1}\left(\frac{1}{p^2+1}\right)=\sin x$

Or $\int_p^{+\infty}\frac{du}{u^2+1}=\left[\arctan u\right]_p^{+\infty}=\frac{\pi}{2}-\arctan p$

La propriété admise donne alors $\mathcal{L}^{-1}\left[\frac{\pi}{2}-\arctan p\right]=\frac{\sin x}{x}$

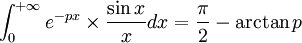
En revenant à la définition de la transformation de Laplace, il vient $\int_0^{+\infty}e^{-px}\times\frac{\sin x}{x}dx=\frac{\pi}{2}-\arctan p$

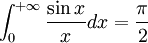En particulier, si $p\to0$ , on obtient $\int_0^{+\infty}\frac{\sin x}{x}dx=\frac{\pi}{2}$ .

Notons qu'une méthode pour démontrer la formule de tranformée de Laplace inverse est d'utiliser la formule des résidus. La méthode de calcul direct est donc, de ce point de vue, préférable.

Portail des mathématiques

Ce document provient de « Int%C3%A9grale de Dirichlet ».

Catégorie : Intégrale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Intégrale De Dirichlet de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Integrale de Dirichlet — Intégrale de Dirichlet L intégrale de Dirichlet est l intégrale de la fonction sinus cardinal sur la demi droite des réels positifs Il s agit d une intégrale impropre semi convergente, c est à dire que la fonction n est pas intégrable au sens… … Wikipédia en Français
Intégrale de dirichlet — L intégrale de Dirichlet est l intégrale de la fonction sinus cardinal sur la demi droite des réels positifs Il s agit d une intégrale impropre semi convergente, c est à dire que la fonction n est pas intégrable au sens généralisé de Riemann,… … Wikipédia en Français
Intégrale de Dirichlet — L intégrale de Dirichlet est l intégrale de la fonction sinus cardinal sur la demi droite des réels positifs Il s agit d une intégrale impropre semi convergente, c est à dire que la fonction n est pas intégrable au sens généralisé de Riemann,… … Wikipédia en Français
Integrale impropre — Intégrale impropre En mathématiques, l intégrale impropre désigne une extension de l intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des… … Wikipédia en Français
Intégrale Impropre — En mathématiques, l intégrale impropre désigne une extension de l intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des véritables intégrales ou… … Wikipédia en Français
Intégrale généralisée — Intégrale impropre En mathématiques, l intégrale impropre désigne une extension de l intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des… … Wikipédia en Français
DIRICHLET (P. G. LEJEUNE-) — Avec son ami et contemporain Jacobi et son cadet de quelques années Kummer, Dirichlet constitue la première génération des mathématiciens allemands après Gauss, dont naturellement ils subissent très fortement l’influence; mais, alors que celui ci … Encyclopédie Universelle
Intégrale impropre — En mathématiques, l intégrale impropre désigne une extension de l intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des véritables intégrales ou… … Wikipédia en Français
Intégrale de Lebesgue — En mathématiques, l’intégrale de Lebesgue désigne à la fois une théorie relative à l intégration et à la mesure, puis le résultat de l intégration d une fonction à valeurs réelles définie sur (ou sur ), munis de la mesure de Lebesgue.… … Wikipédia en Français
Intégrale définie — Table d intégrales Intégrales définies On appelle intégrale définie dans l intervalle [a,b] lorsque est une primitive quelconque de et que et … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Intégrale De Dirichlet