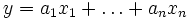- Linearite
-
Linéarité
La linéarité en mathématiques
Les premiers exemples de situations où intervient la linéarité sont les situations de proportionnalité entre deux variables : le graphe représentant une variable en fonction de l'autre forme alors une ligne droite qui passe par l'origine.
Le concept de linéarité s'est ensuite étendu pour désigner un rapport de dépendance très simple entre plusieurs variables : la variable y dépend linéairement des variables x1,...,xn, ou on dit encore qu'elle s'exprime comme combinaison linéaire de ces variables, quand il existe des constantes a1,...,an telles qu'on ait la relation
L'algèbre linéaire est le domaine des mathématiques qui étudie de façon systématique les propriétés associées à la dépendance linéaire. Les concepts de base sont celui de combinaison linéaire précédemment introduit et les notions d'espace vectoriel et d'application linéaire. Ils permettent de définir l'indépendance linéaire et la dimension, c'est-à-dire le comptage du nombre de paramètres nécessaires pour décrire un phénomène linéaire.
Étude du caractère linéaire d'un système physique
La linéarité est un critère déterminant l'aptitude d'un système à avoir une réponse proche d'une droite. Par exemple, la tension aux bornes d'une résistance dépend linéairement de l'intensité la traversant (U = Ri).
Pour déterminer la linéarité, on peut commencer par calculer la droite approchée par la méthode des moindres carrés, par exemple (d'autres méthodes de calcul existent). Ensuite, il suffit de quantifier l'écart de la réponse du système par rapport à cette droite.Voir aussi
- Portail des mathématiques
Catégorie : Vocabulaire des mathématiques
Wikimedia Foundation. 2010.