Indice d'un groupe

Pour les articles homonymes, voir indice.

Définition

Soit $G$ un groupe fini, $H$ un sous-groupe de $G$ et $t$ un nombre naturel strictement positif. Selon le Théorème de Lagrange, on sait que la cardinalité de $H$ divise la cardinalité de $G$ :

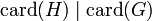$\mbox{card}(H) \mid \mbox{card} (G)$ .

En d'autres termes, on peut aussi écrire :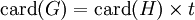

$\mbox{card} (G) = \mbox{card} (H) \times t$ .

Ce nombre naturel $t$ est justement nommé « l'indice de $H$ dans $G$ ». Cet indice est noté :

t = [G : H]

d'où l'écriture du Théorème de Lagrange :

$\mbox{card} (G) = \mbox{card} (H) \times [G:H]$ .

Exemple

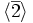Calculons $[\mathbb Z_{10}:\langle\overline 2\rangle ]$ , où $\langle\overline 2\rangle$ est le sous-groupe de 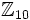$\mathbb Z_{10}$ généré par la classe d'équivalence de 2 $(m o d 10)$ . Ici, l'opération est l'addition usuelle des nombres entiers.

Il faut d'abord trouver la cardinalité de chacun des deux groupes :

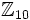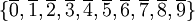On sait que $\mathbb Z_{10}$ est formé de 10 éléments $\{\overline 0 , \overline 1 , \overline 2 , \overline 3 , \overline 4 , \overline 5 , \overline 6 , \overline 7 , \overline 8 , \overline 9 \}$ .

Pour ce qui est de 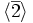$\langle\overline 2\rangle$ , on doit trouver tous les éléments formant le groupe :

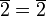
$\overline 2 = \overline 2$

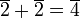
$\overline 2 + \overline 2 = \overline 4$

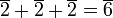
$\overline 2 + \overline 2 + \overline 2 = \overline 6$

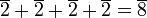
$\overline 2 + \overline 2 + \overline 2 + \overline 2 = \overline 8$

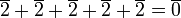$\overline 2 + \overline 2 + \overline 2 + \overline 2 + \overline 2 = \overline 0$ .

Ainsi, le groupe généré par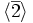 $\langle\overline 2\rangle$ contient 5 éléments.

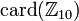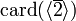Il ne reste qu'à diviser $\mbox{card} (\mathbb Z_{10})$ par $\mbox{card} (\langle\overline 2\rangle)$ , sachant que ces cardinalités sont respectivement 10 et 5.

∴ On a $[\mathbb Z_{10}:\langle\overline 2\rangle ] = 2$ .

Voir aussi

Portail des mathématiques

Ce document provient de « Indice d%27un groupe ».

Catégories : Théorème de mathématiques | Théorie des groupes | Joseph-Louis Lagrange | Groupe fini

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Indice d'un groupe de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Groupe Alterné — En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini de cardinal n. Ce sous groupe est composé des… … Wikipédia en Français
Groupe alterne — Groupe alterné En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini de cardinal n. Ce sous groupe est… … Wikipédia en Français
Groupe alterné — En mathématiques, et plus précisément en théorie des groupes, le groupe alterné de degré n, souvent noté An, est un sous groupe distingué du groupe symétrique des permutations d un ensemble fini à n éléments. Ce sous groupe est composé des… … Wikipédia en Français
Groupe de Janko — En mathématiques, les groupes de Janko J1, J2, J3 et J4 sont quatre des vingt six groupes sporadiques; leurs ordres respectifs sont … Wikipédia en Français
Groupe Symétrique — Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui même. Sommaire 1… … Wikipédia en Français
Groupe de permutation — Groupe symétrique Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui… … Wikipédia en Français
Groupe des permutations — Groupe symétrique Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui… … Wikipédia en Français
Groupe symetrique — Groupe symétrique Cette notion est différente de celle de groupe de symétrie. En mathématiques, plus particulièrement en algèbre, le groupe symétrique d un ensemble E est le groupe des permutations de E, c est à dire des bijections de E sur lui… … Wikipédia en Français
Indice d'abondance des populations d'oiseaux communs — Indice d’abondance des populations d’oiseaux communs STOC ou programme STOC [1] désigne une méthode de production d indices (ou indicateurs) d évolution annuelle de l abondance de différentes espèces d oiseaux communs. Ces indices (via des… … Wikipédia en Français
Groupe Des Classes D'idéaux — En mathématiques, la théorie des corps de nombres fait apparaître un groupe abélien fini construit à partir de chaque tel corps : son groupe des classes d idéaux. Sommaire 1 Histoire et origine du groupe des classes d idéaux 2 Développement… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Indice d'un groupe