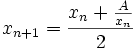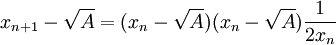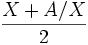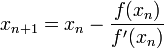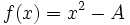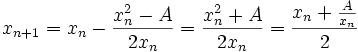Algorithme de Babylone

Algorithme de Babylone

Méthode de Héron

En mathématiques, la méthode de Héron ou méthode babylonienne est une méthode efficace d'extraction de racine carrée. Elle porte le nom du mathématicien Héron d'Alexandrie mais certains calculs antérieurs semblent prouver que la méthode est plus ancienne.

Sommaire

Principe

Pour déterminer la racine carrée du nombre A, on choisit un nombre x0 assez proche de √A, en général la partie entière de √A, puis on construit une suite définie par récurrence par

x_{n+1} = \frac{x_n+ \frac{A}{x_n}}{2}

La suite ainsi obtenue est une suite décroissante à partir du second terme, convergeant vers √A.

La convergence en est quadratique : l'écart entre chaque terme et la limite √A évolue comme le carré de l'écart précédent

x_{n+1}- \sqrt{A} = (x_{n}- \sqrt{A})(x_{n}- \sqrt{A}) \frac{1}{2 x_n}

c’est-à-dire que le nombre de décimales exactes double à chaque itération.

Si le premier terme de la suite est un nombre entier ou rationnel, tous les termes successifs seront des nombres rationnels, ce qui permet d'approcher un nombre irrationnel tel que √2 par une suite de rationnels.

L'algorithme nécessite à chaque étape de faire une division, qui elle-même requiert une suite d'opérations d'autant plus longue que la précision demandée est importante (on suppose qu'on ne dispose pas de machine à calculer, sans quoi l'algorithme serait inutile). Néanmoins, l'algorithme est robuste, il supporte bien quelques approximations (et même quelques erreurs, dont l'effet sera de retarder l'obtention du résultat mais n'empéchera pas de l'obtenir), ce qui permet de se contenter de divisions (pas trop) fausses, au moins au début.

Motivation géométrique

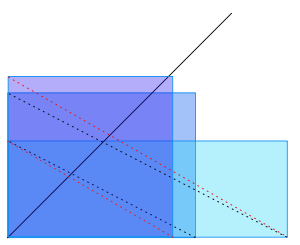
Les rectangles ont même aire, Chaque rectangle a pour longueur la moyenne des dimensions du rectangle précédent

La présentation mathématique actuelle ne permet pas la mise en évidence du principe géométrique. Chez les mathématiciens grecs, extraire la racine carré de A c'est trouver un carré dont l'aire soit A. En prenant un rectangle de côté arbitraire X et de même aire, il est nécessaire que l'autre côté ait pour longueur A/X. Mais ce rectangle n'est pas carré (en général). Pour le rendre moins rectangle, il suffit de prendre un rectangle dont la longueur est la moyenne arithmétique des deux côtés précédents soit

\frac{X+A/X}{2}

et dont l'aire reste A. En réitérant infiniment le processus, on transforme petit à petit le rectangle en carré de même aire

Généralisation de la méthode

Une méthode analogue existe pour extraire la racine nième d'un nombre (voir Algorithme de calcul de la racine n-ième).

La méthode de Héron est un cas particulier de la méthode de Newton. En effet, dans la méthode de Newton, il s'agit de trouver un zéro d'une fonction f en utilisant la récurrence suivante :

x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}

En prenant

f(x) = x^2 - A\,

la récurrence devient

x_{n+1}= x_n - \frac{x_n^2-A}{2x_n} = \frac{x_n^2+A}{2x_n} = \frac{x_n + \frac{A}{x_n} }{2}

Voir aussi


Méthodes de résolution d'équations
Résolution d'équations polynomiales Méthode de Bézout · Méthode de Cardan · Méthode de Sotta · Méthode de Ferrari · Méthode de Descartes · Méthode de Tschirnhaus · Méthode d'Hermite
Recherche d'un zéro Méthode de dichotomie · Méthode de Newton · Méthode de la sécante · Méthode de Müller · Méthode de Brent · Méthode de la fausse position · Méthode de Héron · Méthode de Laguerre · Méthode du cercle de séparation · Méthode de Halley · Méthode de Householder . Méthode de Quasi-Newton


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « M%C3%A9thode de H%C3%A9ron ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algorithme de Babylone de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Méthode de Newton — Isaac Newton En analyse numérique, la méthode de Newton ou méthode de Newton Raphson[1] est, dans son application la plus simple, un algorithme efficace pour trouver numériquement une approximation précise d …   Wikipédia en Français

  • Methode de Newton — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Methode de la corde — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Méthode De Newton — Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Méthode de Newton-Raphson — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Méthode de la corde — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Méthode de newton — Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Racine carrée de deux — La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu’il est multiplié par lui même, donne le nombre 2, autrement dit √2 × √2 = 2. C’est un nombre irrationnel, dont une valeur approchée à 10 9… …   Wikipédia en Français

  • Algèbre géométrique — Pour les articles homonymes, voir Algèbre (homonymie) et notamment la structure mathématique d algèbre géométrique. Paul Tannery popularise l expression algèbre géométrique. En mathématiques, l’algèbre géométrique regroupe …   Wikipédia en Français

  • Constante de Pythagore — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”