- Algorithme De Calcul De La Racine N-ième
-
Algorithme de calcul de la racine n-ième
La racine n-ième d'un nombre réel positif A, notée
![\sqrt[n]{A}](/pictures/frwiki/51/3078170f7aedde3f7a90dcfb305c6533.png) , est le réel positif solution de l'équation
, est le réel positif solution de l'équation- xn = A
(Pour tout entier naturel non nul n, il existe n nombres complexes distincts solutions de cette équation si A > 0, mais une seule est positive et réelle.)
Il existe un algorithme de calcul d'une valeur approchée de la racine n-ième dont la convergence est très rapide:
- Considérer une valeur approchée initiale x0
- Poser
![x_{k+1} = \frac{1}{n} \left[{(n-1)x_k +\frac{A}{x_k^{n-1}}}\right]](/pictures/frwiki/54/609d6ace4927f7ffd374fa504c34e617.png)
- Recommencer à l'étape 2 jusqu'à la précision voulue.
Un cas particulier connu de cet algorithme est la méthode de Héron. Il suffit de remplacer n = 2 dans la formule récurrente à la deuxième étape:
Il existe plusieurs variantes possibles de cet algorithme. Un mouture le considère comme un cas particulier de la méthode de Newton (également appelée méthode de Newton-Raphson) qui permet de trouver des zéros d'une fonction f en partant d'une valeur approchée initiale. Bien que la méthode de Newton soit itérative, ce qui signifie qu'elle approche la solution par une suite de valeurs approchées de plus en plus précises, elle converge très rapidement. La vitesse de convergence est quadratique, ce qui signifie grossièrement que le nombre de décimales exactes (ou nombre de bits exacts) double à chaque itération (améliorant ainsi la précision de la valeur approchée de 1 bit à 64 bits en seulement 6 itérations). Pour cette raison, cet algorithme est souvent employé dans des ordinateurs comme une méthode très rapide pour calculer les racines carrées.
Pour des grandes valeurs de n, l'algorithme de la racine n-ième est légèrement moins efficace puisqu'il exige le calcul de
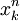 à chaque étape, mais peut être efficacement mis en œuvre avec un bon algorithme d'élévation à une puissance.
à chaque étape, mais peut être efficacement mis en œuvre avec un bon algorithme d'élévation à une puissance.Lien avec la méthode de Newton
La méthode de Newton est une méthode permettant de déterminer une valeur approchée d'un zéro d'une fonction f. Le schéma général de la méthode est le suivant:
- Considérer une valeur approchée de départ x0
- Poser
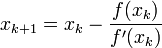
- Recommencer à l'étape 2 jusqu'à la précision voulue.
Le problème de la recherche d'une racine n-ième peut se ramener à celui de la recherche d'un zéro de la fonction f définie par
La fonction f est dérivable sur
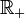 et la dérivée est donnée par:
et la dérivée est donnée par:D'où la relation récurrente:
qui mène à l'algorithme général de recherche d'une racine n-ième.
- Portail des mathématiques
Catégories : Algorithme de recherche d'un zéro d'une fonction | Analyse numérique
Wikimedia Foundation. 2010.

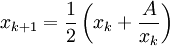
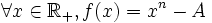
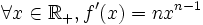
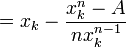
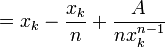
![= \frac{1}{n} \left[{(n-1)x_k +\frac{A}{x_k^{n-1}}}\right]](/pictures/frwiki/99/c6c33a5650ff22b1d76b2584d63ecadc.png)