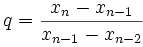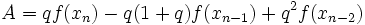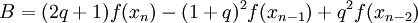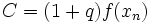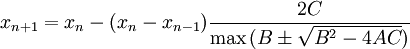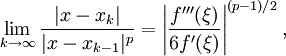Methode de Muller

Methode de Muller

Méthode de Müller

En mathématiques, la méthode de Müller est un algorithme de recherche d'un zéro d'une fonction qui est basé sur la méthode de la sécante mais qui utilise une approximation quadratique d'une partie de la fonction au lieu d'une approximation linéaire. Ceci offre une convergence plus rapide que la méthode de la sécante. Une particularité de cette méthode est que le candidat issu de la recherche peut devenir complexe.

La méthode

La méthode de la sécante définit une relation de récurrence basée sur l'interpolation linéaire entre deux points. La méthode de Müller de par sa nature quadratique, nécessite trois points. On pose ainsi :

q = \frac{x_n - x_{n-1}}{x_{n-1} -x_{n-2}}

On définit ensuite trois termes :

A = qf(x_n) - q(1+q)f(x_{n-1})+q^2f(x_{n-2})~
B = (2q+1)f(x_n) - (1+q)^2 f(x_{n-1}) + q^2 f(x_{n-2})~
C = (1+q)f(x_n)~

La relation de récurrence pour cette méthode est donnée au final par :

x_{n+1} = x_n - (x_n - x_{n-1})\frac{2C}{\max{(B\pm\sqrt{B^2-4AC})}}~

L'initialisation nécessite 3 points x0, x1 et x2 qui sont proches, si possible, de la solution recherchée.

Vitesse de convergence

La vitesse de convergence de la méthode de Müller est approximativement 1,84 contre 1,62 pour la méthode de la sécante et 2 pour la méthode de Newton-Raphson.

Plus précisément, si ξ est une racine simple de f (ainsi f(ξ) = 0 et f'(ξ) ≠ 0), que f est trois fois continuement différentiable et que les points de départ x0, x1, et x2 sont pris suffisamment près de ξ, alors les itérés vérifient

\lim_{k\to\infty} \frac{|x-x_k|}{|x-x_{k-1}|^p} = \left| \frac{f'''(\xi)}{6f'(\xi)} \right|^{(p-1)/2},

où p ≈ 1.84 est la racine positive de x3 − x2 − x − 1 = 0.

Références

  • Muller, David E., "A Method for Solving Algebraic Equations Using an Automatic Computer," MTAC, 10 (1956), 208-215.
  • Atkinson, Kendall E. (1988). An Introduction to Numerical Analysis, 2nd edition, Section 2.4. John Wiley & Sons, New York. ISBN 0-471-50023-2.
  • Burden, R. L. and Faires, J. D. Numerical Analysis, 4th edition, pages 77ff.
  • Press, William H., et al. (1992). Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd edition, page 364. ISBN 052143064X.


Méthodes de résolution d'équations
Résolution d'équations polynomiales Méthode de Bézout · Méthode de Cardan · Méthode de Sotta · Méthode de Ferrari · Méthode de Descartes · Méthode de Tschirnhaus · Méthode d'Hermite
Recherche d'un zéro Méthode de dichotomie · Méthode de Newton · Méthode de la sécante · Méthode de Müller · Méthode de Brent · Méthode de la fausse position · Méthode de Héron · Méthode de Laguerre · Méthode du cercle de séparation · Méthode de Halley · Méthode de Householder . Méthode de Quasi-Newton
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « M%C3%A9thode de M%C3%BCller ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Methode de Muller de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Méthode De Müller — En mathématiques, la méthode de Müller est un algorithme de recherche d un zéro d une fonction qui est basé sur la méthode de la sécante mais qui utilise une approximation quadratique d une partie de la fonction au lieu d une approximation… …   Wikipédia en Français

  • Méthode de müller — En mathématiques, la méthode de Müller est un algorithme de recherche d un zéro d une fonction qui est basé sur la méthode de la sécante mais qui utilise une approximation quadratique d une partie de la fonction au lieu d une approximation… …   Wikipédia en Français

  • Méthode du Muller — Méthode de Müller En mathématiques, la méthode de Müller est un algorithme de recherche d un zéro d une fonction qui est basé sur la méthode de la sécante mais qui utilise une approximation quadratique d une partie de la fonction au lieu d une… …   Wikipédia en Français

  • Méthode de Müller — En mathématiques, la méthode de Müller est un algorithme de recherche d un zéro d une fonction qui est basé sur la méthode de la sécante mais qui utilise une approximation quadratique d une partie de la fonction au lieu d une approximation… …   Wikipédia en Français

  • Methode de Newton — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Methode de la corde — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Méthode De Newton — Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Méthode de Newton-Raphson — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Méthode de la corde — Méthode de Newton Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

  • Méthode de newton — Isaac Newton En analyse numérique, la méthode de Newton, ou méthode de Newton Raphson[1], est un algorithme efficace pour trouver des approximations d un zéro …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”