Clique (Théorie Des Graphes)

Le concept de clique intervient dans la théorie des graphes non-orientés. Le cardinal de la plus grande clique contenue dans un graphe est une caractéristique de ce même graphe, que l'on peut relier au nombre chromatique. La recherche de la plus grande clique d'un graphe (au sens du nombre de sommets) est un problème NP-complet, et à ce titre, un problème modèle en informatique théorique.

Sommaire 1 Définition 2 Problème de la clique 2.1 Énoncé 2.2 Algorithmes 3 Problème de la plus grande clique d'un graphe 4 Notes et références 5 Voir aussi 5.1 Articles connexes 5.2 Liens externes 5.3 Bibliographie

Définition

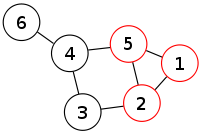
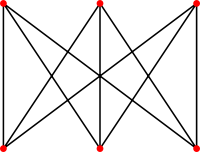
Dans la théorie des graphes, une clique est un ensemble de sommets deux-à-deux adjacents (notion de graphe complet). Mais le terme « clique » est aussi souvent utilisé pour parler du graphe induit par une clique. De même, on désigne couramment par le terme « biclique » un graphe biparti complet plutôt que son ensemble de sommets ou d'arêtes.

On utilise parfois le terme p-clique ou encore clique de cardinalité p pour désigner une clique contenant p nœuds.

Problème de la clique

Énoncé

Il s'agit d'établir si un graphe G donné contient une clique de cardinal au moins égal à un entier donné k. Lorsqu'on a constitué une liste de k sommets, il est trivial de vérifier s'ils forment une clique, et c'est pourquoi ce problème est de type NP-complet.

La recherche d'une clique dans un graphe revient aussi à rechercher un stable dans le graphe complémentaire. Ce dernier graphe s'obtient en enlevant les arêtes du graphe G et en rajoutant toutes les arêtes reliant les sommets, qui n'y étaient pas.

Ainsi, le caractère « NP-complet » du problème de la clique résulte directement du caractère NP-complet du problème du « stable », parce que dire qu'un graphe contient une clique de taille k, revient à affirmer qu'il existe un stable de cardinal k dans le graphe complémentaire : en effet, si un sous-graphe est complet, le sous-graphe complément n'a pas d'arêtes.

Algorithmes

La recherche exhaustive d'une k-clique à l'intérieur d'un graphe procédera par examen de tous les sous-graphes de taille k, en testant s'ils forment une clique. Toutefois, le nombre de sous-graphes de taille k dans un graphe à n sommets peut être très élevé : il est égal à .

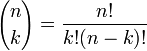Une heuristique consiste à considérer chaque sommet comme une 1-clique (une clique de cardinal 1), et à former des cliques de tailles croissantes par réunion de deux cliques connues jusqu'à ce qu'il n'y ait plus plus de réunion possible. On pourra réunir deux cliques A et B si tout sommet de la clique A est adjacent à chaque sommet de la clique B. Cette heuristique s'exécute à un coût linéaire (fonction linéaire du nombre de sommets du graphe), mais elle peut passer à côté d’une grande clique, parce que deux ou plusieurs sommets de cette « clique intéressante » auront déjà été regroupés à une étape antérieure avec des sommets qui n'appartiennent pas à cette clique. On peut implanter avantageusement cet algorithme grâce à la stratégie « Union-Find ».

Certains cas particuliers peuvent être résolus à un coût sous-exponentiel. Pour k = 3, il existe un algorithme de complexité O(n^1.41) où n est le nombre de sommets du graphe.^[1]

Problème de la plus grande clique d'un graphe

Le problème d'optimisation associé au « problème de la clique » est le problème de la clique maximum : il consiste à trouver la plus grande clique (au sens de son cardinal) dans un graphe. La recherche dans un graphe d'une clique de taille maximale est un problème classique de la théorie de la complexité. Cette taille maximale minore alors le nombre chromatique du graphe.

Le problème de la clique maximum fait partie des 21 problèmes NP-complets de Karp publiés en 1972 dans Reducibility Among Combinatorial Problems. L'article didactique de Cook sur les problèmes NP-complets le mentionne aussi.

Notes et références

Voir aussi

Articles connexes

• Combinatoire
• Théorie de Ramsey
• Theorem on friends and strangers

Liens externes

• (en) Études de cas instructives pour le problème de la clique maximum, du « stable » maximum, du graphe recouvrant minimum et du coloriage des arêtes

Bibliographie

• Claude Berge, Théorie des Graphes, éditions Dunod, 1958, 250 p., « 4. Les nombres fondamentaux de la théorie des graphes » 
• M. Gondran, M. Minoux, Graphes et algorithmes, éditions Eyrolles, coll. « Dir. Ét. & Rech. EDF », 1979 (réimpr. 1985), 546 p. 
• Cook, Stephen A. (1971). "The Complexity of Theorem-Proving Procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing: 151-158. Consulté le 2007-06-11. 
• Karp, Richard (1972). "Reducibility Among Combinatorial Problems". Proceedings of a Symposium on the Complexity of Computer Computations, Plenum Press. 
• Michael R. Garey, David S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, vol. A1.2: GT19, W.H. Freeman, 1979 (ISBN 0-7167-1045-5), p. 194 

• Portail des mathématiques