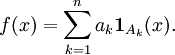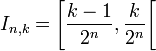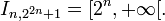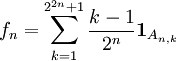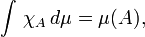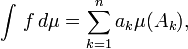Fonction Étagée

Fonction Étagée

Fonction étagée

En mathématiques, une fonction étagée est une fonction mesurable dont l'image est finie. De façon équivalente, c'est une fonction simple mesurable. Ces fonctions jouent un rôle important en théorie de l'intégration au sens de Lebesgue. Il s'agit d'une généralisation des fonctions en escalier utilisée en théorie de l'intégrale de Riemann ou de Kurzweil-Henstock.

Sommaire

Propriété caractéristique

Une fonction étagée est une combinaison linéaire (donc finie) de fonctions caractéristiques d'ensembles mesurables. Autrement dit, soient (X, Σ) un espace mesurable, A1, ..., An ∈ Σ une suite finie d'ensembles mesurables, et a1, ..., an une suite finie de nombres réels ou complexes. Une fonction étagée est une fonction de la forme :

f(x)=\sum_{k=1}^n a_k {\mathbf 1}_{A_k}(x).

Ensemble des fonctions étagées

Structure

Il découle de la définition que la somme, le produit de deux fonctions étagées, le produit d'une fonction étagée par un complexe, sont des fonctions étagées. L'ensemble des fonctions étagées constitue donc une C-algèbre commutative.

Densité

Théorème — L'ensemble des fonctions étagées positives est dense dans l'ensemble des fonctions mesurables positives.

Ou de manière équivalente, toute fonction mesurable est la limite simple de fonctions étagées.

Démonstration

Soit f une fonction positive définie sur un espace mesurée 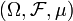(\Omega, {\mathcal F},\mu). Pour tout 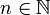n\in\mathbb N, on partage l'image de f en 22n + 1 intervalles de longueur 2 − n. On pose

I_{n,k}=\left[\frac{k-1}{2^n},\frac{k}{2^n}\right[

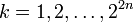pour k=1,2,\ldots,2^{2n} et

I_{n,2^{2n}+1}=[2^n,+\infty[.

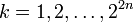On définit les ensembles mesurables An,k = f − 1(In,k) pour k=1,2,\ldots,2^{2n}.

On remarque alors que la suite croissante de fonctions

f_n=\sum_{k=1}^{2^{2n}+1}\frac{k-1}{2^n}{\mathbf 1}_{A_{n,k}}

converge simplement vers f lorsque n tend vers +\infty.

Remarque : si f est bornée, la suite donnée dans la démonstration ci-dessus converge uniformément.

Intégration d'une fonction étagée

En théorie de la mesure, définir l'intégrale d'une fonction étagée est le premier ou le deuxième pas de la définition de l'intégrale par rapport à une mesure. Soit une mesure μ définie sur 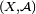\scriptstyle\ \left(X,\mathcal{A}\right). Pour 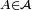\scriptstyle\ A\in \mathcal{A}\ , on pose

\int\,\chi_A\,d\mu=\mu(A),

puis

\int\,f\,d\mu=\sum_{k=1}^na_k\mu(A_k),

lorsque chaque terme de la somme ci-dessus est fini. Ainsi les fonctions étagées sont à la théorie de l'intégration de Lebesgue ce que les fonctions en escalier sont à l'intégration de Riemann ou de Kurzweil-Henstock. 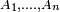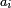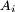Par exemple, dans le cas particulier où \scriptstyle\ A_1,....,A_n sont des intervalles contigus de même longueur, et où les \scriptstyle\ a_i sont les évaluations d'une fonction \scriptstyle\ g au début des intervalles \scriptstyle\ A_i, l'expression 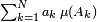\scriptstyle\ \sum_{k=1}^N a_k\,\mu(A_k)\ est appelée somme de Riemann.

Voir aussi


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction %C3%A9tag%C3%A9e ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction Étagée de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Fonction etagee — Fonction étagée En mathématiques, une fonction étagée est une fonction mesurable dont l image est finie. De façon équivalente, c est une fonction simple mesurable. Ces fonctions jouent un rôle important en théorie de l intégration au sens de… …   Wikipédia en Français

  • Fonction étagée — En mathématiques et en analyse : Une fonction simple est une fonction numérique dont l image est constituée d’un nombre fini de valeurs réelles (ou éventuellement complexes). Une fonction étagée est une fonction simple définie sur un espace… …   Wikipédia en Français

  • Fonction Caractéristique (Mathématiques) — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction caracteristique (mathematiques) — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction caractéristique (mathématiques) — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction caractéristique d'un ensembel — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction indicatrice — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction Simple — Une fonction simple sur un ensemble E est une fonction numérique qui ne prend qu un nombre fini de valeurs, i.e. l ensemble f(E) est fini. Caractérisation des fonctions simples Les fonctions simples sont les combinaisons linéaires de fonctions… …   Wikipédia en Français

  • Fonction simple — Une fonction simple sur un ensemble E est une fonction numérique qui ne prend qu un nombre fini de valeurs, i.e. l ensemble f(E) est fini. Caractérisation des fonctions simples Les fonctions simples sont les combinaisons linéaires de fonctions… …   Wikipédia en Français

  • Fonction caractéristique (théorie des ensembles) — Cet article concerne les fonctions caractéristiques en théorie des ensembles. Pour les articles homonymes, voir Fonction caractéristique. Pour les fonctions indicatrices en analyse convexe, voir Fonction indicatrice (analyse convexe) …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”