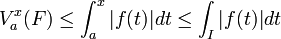Fonction À Variation Bornée
- Fonction À Variation Bornée
-
Fonction à variation bornée
En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de Dirichlet sur la convergence des séries de Fourier.
Définition
Soit f une fonction définie sur le compact [a,b] à valeur dans  .
.
Pour chaque subdivision ![\sigma =(a=x_0 ,x_1 ,\ldots ,x_n =b) \in \mathcal S ([a,b])](/pictures/frwiki/49/1eb41fc962e7768a965a97a5c9865013.png) , on définit V(f,σ) par :
, on définit V(f,σ) par :
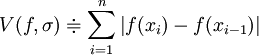 .
.
On appelle variation totale de f la valeur 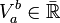 définie par :
définie par :
![V^{b}_{a}(f) \doteqdot \sup_{\sigma \in \mathcal S ([a,b])} V(f,\sigma )](/pictures/frwiki/57/9030b5fc7c1818b6bde05f4ebbc1e7da.png)
On dit que f est à variation bornée si 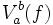 est fini.
est fini.
Plus généralement, une fonction définie sur un intervalle quelconque est à variation bornée si 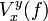 est fini quels que soient x et y dans l'intervalle.
est fini quels que soient x et y dans l'intervalle.
Propriétés
- Les fonctions à variation bornée forment un sous-espace vectoriel de l'espace des fonctions de [a,b] dans
 .
.
- Toute fonction de classe
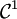 est à variation bornée, toute fonction monotone également.
est à variation bornée, toute fonction monotone également.
- Toute fonction à variation bornée est limite uniforme d'une suite de fonctions en escalier.
- Toute fonction à variation bornée est différence de deux fonctions croissantes. A fortiori, l'espace vectoriel des fonctions à variation bornée est engendré par l'ensemble des fonctions croissantes ; on en déduit également que les fonctions à variation bornée ont au plus une infinité dénombrable de points de discontinuité et sont dérivables presque partout (au sens de la mesure de Lebesgue).
- Si f est intégrable au sens de Lebesgue sur un intervalle I, alors, pour a fixé dans I la fonction
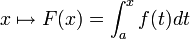 est à variation bornée. En effet,
est à variation bornée. En effet, 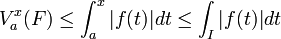
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Analyse réelle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Fonction À Variation Bornée de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Fonction a variation bornee — Fonction à variation bornée En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de… … Wikipédia en Français
Fonction à variation bornée — En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de Dirichlet sur la convergence… … Wikipédia en Français
Fonction absolument continue — Absolue continuité En mathématiques, on introduit les notions de fonction absolument continue et de mesure absolument continue. Ces deux concepts entretiennent des rapports. Sommaire 1 Fonction absolument continue 1.1 Motivation 1.2 Définition … Wikipédia en Français
Fonction Entière — La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le plan complexe. C … Wikipédia en Français
Fonction entiere — Fonction entière La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le … Wikipédia en Français
Fonction entière — La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le plan complexe. C … Wikipédia en Français
Fonction Zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… … Wikipédia en Français
Fonction Zêta De Riemann — En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des nombres premiers. Elle est… … Wikipédia en Français
Fonction dzêta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… … Wikipédia en Français
Fonction zeta de Riemann — Fonction zêta de Riemann En mathématiques, la fonction ζ de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des… … Wikipédia en Français
 .
.![\sigma =(a=x_0 ,x_1 ,\ldots ,x_n =b) \in \mathcal S ([a,b])](/pictures/frwiki/49/1eb41fc962e7768a965a97a5c9865013.png) , on définit V(f,σ) par :
, on définit V(f,σ) par :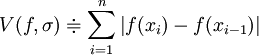 .
.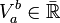 définie par :
définie par :![V^{b}_{a}(f) \doteqdot \sup_{\sigma \in \mathcal S ([a,b])} V(f,\sigma )](/pictures/frwiki/57/9030b5fc7c1818b6bde05f4ebbc1e7da.png)
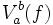 est fini.
est fini.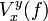 est fini quels que soient x et y dans l'intervalle.
est fini quels que soient x et y dans l'intervalle. .
.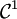 est à variation bornée, toute fonction monotone également.
est à variation bornée, toute fonction monotone également.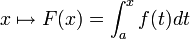 est à variation bornée. En effet,
est à variation bornée. En effet,