Mesure (mathématique)

Pour les articles homonymes, voir mesure.

En mathématiques, une mesure est une fonction qui associe une « longueur », un « volume » ou encore une « probabilité » à certaines parties d'un ensemble donné. Il s'agit d'un important concept en analyse et en théorie des probabilités. Formellement, une mesure μ est une fonction qui associe à chaque élément S d'une σ-algèbre donnée X une valeur μ(S), qui est un réel positif ou l'infini. Les propriétés suivantes doivent être vérifiées :

• L'ensemble vide a une mesure nulle : ,
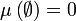• La mesure est σ-additive : si E₁, E₂, … sont des ensembles appartenant à X, en quantité dénombrable et deux à deux disjoints, et si E est leur réunion, alors la mesure μ(E) est égale à la somme .

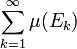Entre autres, µ(E₁ ∪ E₂) = µ(E₁) + µ(E₂).

Lorsque μ est une mesure sur la σ-algèbre X, un élément de X est dit μ-mesurable, ou plus simplement mesurable. Un ensemble Ω conjointement avec une σ-algèbre X sur Ω et une mesure μ sur X forment ce que l'on appelle un espace mesuré, noté (Ω, X, μ).

Les propriétés suivantes peuvent être obtenues à partir des axiomes précédents :

• Si E₁ et E₂ sont deux ensembles mesurables tels que E₁ est un sous-ensemble de E₂, alors μ(E₁) ≤ μ(E₂).
• Si E₁, E₂, E₃, ... sont des ensembles mesurables et si E_n est un sous-ensemble de E_n+1 pour tout n, alors la réunion E des ensembles E_n est mesurable et μ(E) = lim μ(E_n).
• Si E₁, E₂, E₃, ... sont des ensembles mesurables et si, pour tout n, E_n+1 est un sous-ensemble de E_n, alors l'intersection E des ensembles E_n est mesurable ; de plus, si au moins l'un des ensembles E_n a une mesure finie, alors μ(E) = lim μ(E_n).

Un ensemble S est dit presque vide ou négligeable lorsqu'il est inclus dans une partie mesurable T telle μ(T) = 0. La mesure μ est dite complète lorsque tout sous-ensemble d'un ensemble presque vide est mesurable (un tel sous-ensemble est automatiquement lui-même presque vide).

Exemples

Voici quelques exemples importants de mesure :

• La mesure nulle est définie par μ(S) = 0 pour tout S.
• La mesure de dénombrement (ou de comptage) est définie par μ(S) = nombre d'éléments dans S.
• La mesure de Lebesgue est l'unique mesure complète invariante par translation sur une σ-algèbre contenant les intervalles de telle que μ([0,1]) = 1.
• La mesure de Haar pour un groupe topologique localement compact est une généralisation de la mesure de Lebesgue et a une propriété d'unicité similaire.
• La mesure de Hausdorff utilisée dans le monde des fractales.
• La mesure de Dirac μ_a défini par μ_a(S) = χ_S(a), où χ_S la fonction indicatrice de S. La mesure d'un ensemble est égale à 1 si celui-ci contient le point a et à 0 sinon.
• Un espace probabilisable est un espace mesuré sur lequel il existe une mesure qui prend la valeur 1 sur l'univers tout entier (et ainsi prend toutes ses valeurs dans le segment [0, 1]). Une telle mesure est appelée une mesure de probabilité. L'espace probabilisable, une fois muni d'une telle mesure, est un espace probabilisé. Voir les axiomes des probabilités.

Généralisation

Dans certains cas, il est utile d'avoir une « mesure » dont les valeurs ne sont pas restreintes aux réels positifs et à l'infini. Par exemple, une fonction σ-additive définie sur des ensembles et qui prend des valeurs réelles est appelée mesure signée, tandis qu'une telle fonction qui prend des valeurs complexes est appelée mesure complexe. Une mesure qui prend des valeurs dans un espace de Banach est appelée mesure spectrale ; celles-ci sont principalement utilisés en analyse fonctionnelle pour le théorème spectral.

Une autre généralisation est la notion de mesure additive ou moyenne. La définition est la même que celle d'une mesure sauf que la σ-additivité est remplacée par l'additivité finie. Historiquement, cette définition fut introduite en premier, mais s'avéra dans la pratique peu utile. Cette notion est utile pour étudier le paradoxe de Banach-Tarski et ses généralisations.

Un résultat remarquable en géométrie intégrale, connu sous le nom du théorème de Hadwiger, affirme que l'espace des fonctionnelles invariantes par translation, additives, qui sont des fonctions d'ensembles pas forcément positives et définies sur des réunions d'ensembles compacts convexes dans , est constitué (à un multiple scalaire près) de « mesures » qui sont homogènes de degré k pour chaque k = 0,1,2,...,n, et de combinaisons linéaires de ces « mesures ».

L'« homogénéité du degré k » signifie qu' « élargir » n'importe quel ensemble par n'importe quel facteur c>0 multiplie la « mesure » de l'ensemble par c^k. La seule qui soit homogène de degré n correspond au volume ordinaire en dimension n. La seule qui est homogène de degré n-1 représente le « volume de surface » et est appelée mesure superficielle. Celle qui est homogène de degré 1 est une fonction mystérieuse appelée la « largeur moyenne ». Celle qui est homogène de degré 0 est la caractéristique d'Euler.

Articles connexes

• Théorie de la mesure
• Théorie géométrique de la mesure
• Presque partout
• Théorie ergodique
• Paradoxe de Banach-Tarski, qui nécessite l'axiome du choix
• Mesures secondaires

• Portail des mathématiques