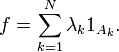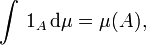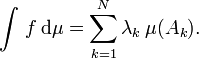Fonction simple

Fonction simple

Fonction simple

Une fonction simple sur un ensemble E est une fonction numérique qui ne prend qu'un nombre fini de valeurs, i.e. l'ensemble f(E) est fini.

Caractérisation des fonctions simples

Les fonctions simples sont les combinaisons linéaires de fonctions indicatrices. En effet, supposons que

f=\sum_{k=1}^N \lambda_k 1_{A_k}.

On a alors

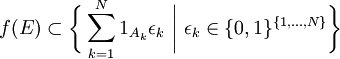f(E)\subset \biggl\{\sum_{k=1}^N1_{A_k}\epsilon_k \ \bigg|\ \epsilon_k \in \{ 0 ,1 \}^{ \{1,...,N \}} \biggr\}.

Supposons que f(E) est fini et notons a1,...aN les valeurs non nulles de f, on pose Aj = f − 1(aj) alors les ensembles A1,....,AN sont 2 à 2 disjoints et on a

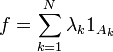f=\sum_{k=1}^N \lambda_k 1_{A_k}.

Fonctions simples et fonctions étagées en théorie de la mesure

En théorie de la mesure, définir l'intégrale d'une fonction simple est le premier ou le deuxième pas de la définition de l'intégrale par rapport à une mesure. Pour une mesure μ, on pose

\int\,1_A\,\mathrm d\mu=\mu(A),

puis

\int\,f\,\mathrm d\mu=\sum_{k=1}^N \lambda_k\,\mu(A_k).

On suppose pour cela que les ensembles concernés A,A1,....,AN appartiennent à la tribu sur laquelle la mesure μ est définie : on dit que la fonction f est mesurable. Ainsi les fonctions simples mesurables (fonctions étagées) sont à la théorie de l'intégration de Lebesgue ce que les fonctions en escalier sont à l'intégration de Riemann. Par exemple, dans le cas particulier où A1,....,AN sont des intervalles contigus de même longueur, et où les λi sont les évaluations d'une fonction f au début des intervalles Ai, l'expression 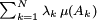\scriptstyle\sum_{k=1}^N \lambda_k\,\mu(A_k) est appelée somme de Riemann.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction simple ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction simple de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Fonction Simple — Une fonction simple sur un ensemble E est une fonction numérique qui ne prend qu un nombre fini de valeurs, i.e. l ensemble f(E) est fini. Caractérisation des fonctions simples Les fonctions simples sont les combinaisons linéaires de fonctions… …   Wikipédia en Français

  • Fonction etagee — Fonction étagée En mathématiques, une fonction étagée est une fonction mesurable dont l image est finie. De façon équivalente, c est une fonction simple mesurable. Ces fonctions jouent un rôle important en théorie de l intégration au sens de… …   Wikipédia en Français

  • Fonction Étagée — En mathématiques, une fonction étagée est une fonction mesurable dont l image est finie. De façon équivalente, c est une fonction simple mesurable. Ces fonctions jouent un rôle important en théorie de l intégration au sens de Lebesgue. Il s agit… …   Wikipédia en Français

  • Fonction Caractéristique (Mathématiques) — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction caracteristique (mathematiques) — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction caractéristique (mathématiques) — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction caractéristique d'un ensembel — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction indicatrice — Fonction caractéristique (théorie des ensembles) Pour les articles homonymes, voir Fonction caractéristique. Le graphe de la fonction indicatrice d un sous ensemb …   Wikipédia en Français

  • Fonction étagée — En mathématiques et en analyse : Une fonction simple est une fonction numérique dont l image est constituée d’un nombre fini de valeurs réelles (ou éventuellement complexes). Une fonction étagée est une fonction simple définie sur un espace… …   Wikipédia en Français

  • Fonction caractéristique (théorie des ensembles) — Cet article concerne les fonctions caractéristiques en théorie des ensembles. Pour les articles homonymes, voir Fonction caractéristique. Pour les fonctions indicatrices en analyse convexe, voir Fonction indicatrice (analyse convexe) …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”