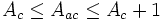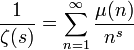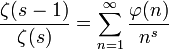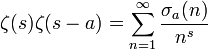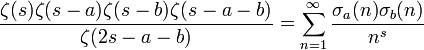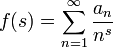- Serie de Dirichlet
-
Série de Dirichlet
 Johann Peter Gustav Lejeune Dirichlet analyse les séries qui portent son nom en 1837 pour démontrer le théorème de la progression arithmétique.
Johann Peter Gustav Lejeune Dirichlet analyse les séries qui portent son nom en 1837 pour démontrer le théorème de la progression arithmétique.
En mathématiques, une série de Dirichlet est une série f(s) de fonctions, définie sur l'ensemble des nombres complexes, noté C dans cet article, et d'une des deux formes suivantes :
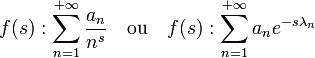
Ici, la suite (λn) est réelle, positive, strictement croissante et non bornée. Le domaine de convergence absolue d'une série de Dirichlet est un demi-plan ouvert de C, limité par une droite dont tous les points ont même abscisse. Ce domaine peut-être vide ou égal à C tout entier. Le domaine de convergence simple est de même nature. Sur le domaine de convergence simple, la fonction définie par la série est holomorphe. Si la partie réelle de s tend vers plus l'infini, la fonction somme, si elle existe, tend vers 0.
Les séries de Dirichlet interviennent en théorie analytique des nombres. Le mathématicien Johann Peter Gustav Lejeune Dirichlet en analyse certaines en 1837 pour démontrer le théorème de la progression arithmétique[1]. L'hypothèse de Riemann s'exprime en termes de zéros du prolongement analytique d'une fonction somme d'une série de Dirichlet.
Sommaire
Définitions et exemples
Définitions
Il existe deux définitions différentes des séries de Dirichlet :
-
- Une série de Dirichlet est une série de la forme suivante, où (an) désigne une suite de nombres complexes[2] :
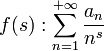
Il existe une définition plus générale :
-
- Une série de Dirichlet est une série de la forme suivante, où (an) désigne une suite de nombres complexes et (λn) une suite réelle, positive, strictement croissante et non bornée.[3] :
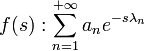
Si l'article traite surtout des séries de Dirichlet répondant à la deuxième définition, en première lecture il est possible de ne considérer que le cas où la suite (λn) est égale à la suite (ln(n)), ce qui ramène à la première définition, moins abstraite.
Exemples
Si les valeurs λn vérifient : λn = n et que l'on note z = e-s, la série prend la forme :
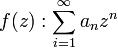
On retrouve la définition d'une série entière, à une constante additive près[Note 1]. Un exemple un peu du même ordre est donnée dans le cas où λn = 2πn, le changement de variable s = -i.t montre qu'une série de Fourier est aussi un cas particulier de série de Dirichlet. La suite de l'article montre que les séries de Dirichlet représente une classe plus générale de séries et les résultats spécifiques aux séries précédentes ne se généralisent pas nécessairement.
Un autre exemple correspond à la première définition, si (λn) = (ln(n)). Il correspond à la définition historique de la série de Dirichlet. La série de Riemann, définie à l'aide de la suite (an) = (1) est un cas particulier. Il correspond à la formule :
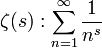
Abscisses de convergences
Abscisse de convergence simple
Soit Cf l'ensemble des nombres réels a tels que la série f(a +i.b) converge pour au moins un réel b. Cet ensemble permet la définition[4] :
- L'abscisse de convergence simple, encore appelée abscisse de convergence est la borne inférieure de l'ensemble Cf. Si Cf n'est pas bornée inférieurement, l'abscisse de convergence est notée -∞ et si Cf est vide, l'abscisse vaut +∞.
Cette abscisse de convergence est l'objet d'une proposition :
-
- Sur le demi-plan ouvert des points complexes de parties réelles strictement supérieures à l'abscisse de convergence simple, la série f est convergente. Sur l'intérieur du demi-plan complémentaire, la série diverge. La convergence est uniforme sur l'ensemble D des points s tel que s - s0 soit un nombre complexe d'argument élément de l'intervalle ]-θ, θ[, avec 0 < θ < π/2. Ici, s0 désigne un point tel que la série f(s0) converge[4].
Il est possible d'évaluer l'abscisse de convergence simple d'une série de Dirichlet :
-
- Soit N la limite supérieure suivante :
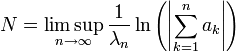
- Si N est strictement supérieur à 0, l'abscisse de convergence simple est égale à N, sinon elle est négative[5].
Une deuxième proposition traite du cas où l'abscisse de convergence simple est strictement négative :
-
- Si l'abscisse de convergence simple d'une série de Dirichlet est strictement négative, elle est égale à la limite suivante[6] :
 Démonstrations
Démonstrations-
- Convergence uniforme :
Soit ε un réel strictement positif et s un élément de D, l'objectif est de montrer que :

Soit s un point de D, pour démontrer la proposition on utilise une technique proche de transformation d'Abel. Soient :

On dispose des égalités, si p est strictement plus petit que q :
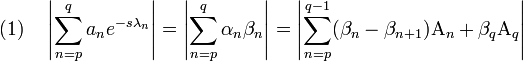
Majorons les facteurs du membre de droite de l'égalité (1) :
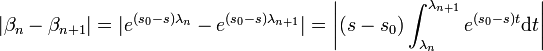
Donc :
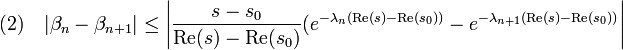
La convergence de la série de Dirichlet en s0 montre que si N est choisi suffisamment grand :
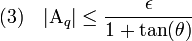
Il suffit alors de remarquer que, dans la somme (1) les termes se détruisent deux à deux (principe d'une somme d'Abel), les majorations (2) et (3) montrent que :
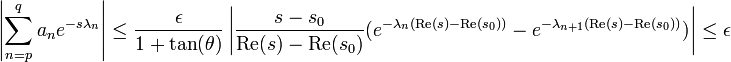
L'application du critère de Cauchy termine la démonstration.
-
- Si N est strictement supérieur à 0, l'abscisse de convergence simple est égale à N, sinon elle est négative :
-
-
- Cas où N est négative :
-
- Si la limite N est négative, cela signifie que la série de terme générale (an) admet pour limite 0. On en déduit qu'au point 0, la série de Dirichlet est convergente et le résultat précédent montre que l'abscisse de convergence est négative.
-
-
- Si N est strictement supérieur à 0, l'abscisse de convergence est plus grande ou égale à N :
-
- Le raisonnement est un peu de même nature que celui utilisé pour démontrer la convergence uniforme. Soit ε un réel strictement positif, par définition de N, il existe un entier n0 tel que :

- La méthode consiste à montrer que la série de Dirichlet converge au point s = N + 2.ε en appliquant encore le critère de Cauchy. Soit p et q deux entiers tels que n0 < q < . La transformation d'Abel montre les majorations :
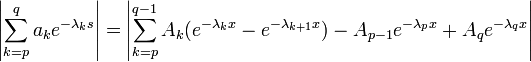
- La majoration (1) montre que :
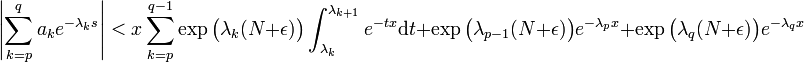
- La définition de x, ainsi que le fait que la suite (λn) soit strictement croissante montre que :
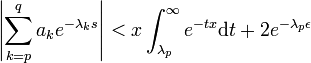
- Le terme de droite est aussi petit que souhaité, si λp et ε sont bien choisis. Le critère de Cauchy permet de conclure.
-
- Si s0 est élément du domaine de convergence de la série de Dirichlet la partie réelle du nombre complexe est plus grande que N :
- Soit M un majorant strictement positif des modules sommes partielles de la série de Dirichlet en s0. La transformation d'Abel montre que :

- On en déduit :
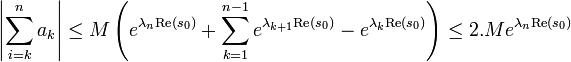
- Ce qui montre que :
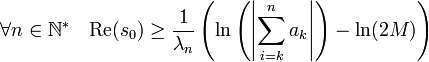
- La partie entière de s0 est bien plus grande que N, ce qui termine la démonstration.
Abscisse de convergence absolue
De même il y a un domaine de convergence absolue DAC et une abscisse de convergence absolue Aac. Les deux abscisses sont liées par les inégalités
Voici deux exemples de résultats sur les abscisses de convergence et de convergence absolue :
- Supposons que
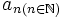 soit une suite bornée de nombres complexes. Alors la série est absolument convergente sur le demi-plan ouvert de s tel que Re(s) > 1.
soit une suite bornée de nombres complexes. Alors la série est absolument convergente sur le demi-plan ouvert de s tel que Re(s) > 1.
- Si l'ensemble des sommes
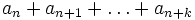 est borné pour n et k ≥ 0, alors la série converge sur le demi-plan ouvert de s tel que Re(s) > 0.
est borné pour n et k ≥ 0, alors la série converge sur le demi-plan ouvert de s tel que Re(s) > 0.
Exemples de décompositions en séries de Dirichlet
où
 est la fonction de Möbius,
est la fonction de Möbius,où
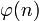 est l'indicatrice d'Euler, et
est l'indicatrice d'Euler, etoù
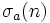 est la fonction diviseur
est la fonction diviseurPropriétés analytiques des séries de Dirichlet
Soit une suite
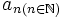 de nombres complexes, nous essayons d'examiner la valeur de
de nombres complexes, nous essayons d'examiner la valeur decomme une fonction de la variable complexe s. Pour que cela prenne un sens, nous avons besoin d'examiner les propriétés de convergence de la série ci-dessus.
Propriétés de la fonction somme
Théorème : la fonction f est une fonction analytique sur le demi-plan ouvert de convergence.
Dans beaucoup de cas, la fonction analytique associée à une série de Dirichlet possède un prolongement analytique sur un domaine plus large. Ceci est le cas pour la fonction zêta :
Théorème. La fonction zêta possède un prolongement méromorphe sur
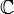 avec un unique pôle à s=1.
avec un unique pôle à s=1.Une des conjectures les plus importantes et non-résolues des mathématiques appelée l'hypothèse de Riemann concerne les zéros de la fonction zêta.
Historique
Définies par Lejeune-Dirichlet en 1837 avec lesquelles il démontra le théorème de la progression arithmétique selon lequel il existe une infinité de nombres premiers dans toute progression arithmétique an+b dès que a et b sont premiers entre eux, ces séries ne furent étudiées qu'à partir des travaux de Emile Cahen qui en fit son sujet de thèse en 1894. Mais sa thèse fut l'objet de nombreuses critiques et provoqua ainsi de nouveaux travaux. La définition des fonctions presque périodiques par Harald Bohr permit de montrer que les fonctions définies par les séries de Dirichlet à coefficients positifs sont presque périodiques dans le demi-plan de convergence absolue.
Une partie du développement de la théorie, vue sous l'angle historique se trouve sous ce lien.
Article détaillé : Histoire de la fonction zêta de Riemann.Annexes
Notes
- ↑ Selon cette définition, la série entière est nulle en 0.
Références
- ↑ Dirichlet Beweis eines Satzes über die arithmetische Progression Bericht über die Verhandlungen der Königlich Preussischen Akademie der Wissenschaften, S. 108-110 p.307-312 1837
- ↑ V&F Bayart, Série de Dirichlet par le site Bibmath.net
- ↑ M. Blambert sur l'abscisse de convergence simple des séries de Dirichlet générales, Ann. Inst. Fourier, Grenoble 14 2 (1964) pp 509-518
- ↑ a et b V. Petkov A. Yger Singularités analytiques des séries de Dirichlet de l'Univeristé de Bordeaux (2001) p 4
- ↑ V. Petkov A. Yger Singularités analytiques des séries de Dirichlet de l'Univeristé de Bordeaux (2001) p 8
- ↑ V. Petkov A. Yger Singularités analytiques des séries de Dirichlet de l'Univeristé de Bordeaux (2001) p 7
Bibliographie
- Apostol, Modular functions and Dirichlet series in number theory, Graduate texts in mathematics 41,Springer, 1990
- Bernstein, Leçons sur les progrès récents de la théorie des séries de Dirichlet, 1933
- Colin, Les séries de Dirichlet, magistère de Cachan, 1995-1996
- Hardy & Riesz, The general theory of Dirichlet's series, Cambridge tracts in mathematics, 1915
- Mandelbrojt, Séries de Dirichlet. Principes et méthodes, Gauthier-Villars, Paris, 1969
- Titschmarsh, The theory of function, Oxford university press, London, 1939
- Portail des mathématiques
Catégories : Analyse complexe | Fonction zêta | Série | Théorie analytique des nombres -
Wikimedia Foundation. 2010.