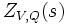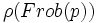Fonction Zeta De Hasse-Weil

Fonction Zeta De Hasse-Weil

Fonction zêta de Hasse-Weil

En mathématiques, la fonction zêta de Hasse-Weil attachée à une variété algébrique V définie sur un corps de nombres K est un des deux types les plus importants des fonctions L. De telles fonctions L sont appelées 'globales', elles sont définies comme des produits eulériens en termes de fonctions zêta locales. Elles forment une des deux classes majeures des fonctions L globales, l'autre étant les fonctions L associées aux représentations automorphes. Conjecturellement, il existe simplement un type essentiel de fonction L globale, avec deux descriptions (provenant d'une variété algébrique, provenant d'une représentation automorphe); ce serait une vaste généralisation de la conjecture de Taniyama-Shimura, elle-même un résultat récent et très profond (en 2004) de la théorie des nombres.

La description d'une fonction zêta de Hasse-Weil comme produit eulérien est relativement simple, au moins à un nombre fini de facteurs près. Ceci découle des suggestions initiales de Helmut Hasse et André Weil, motivées par le cas dans lequel V est un point isolé, et les résultats de la fonction zêta de Riemann.

En prenant le cas où K est le corps des nombres rationnels Q, et V une variété projective non-singulière, nous pouvons pour presque tous les nombres premiers p considérer la réduction de V modulo p, une variété algébrique Vp sur le corps fini 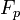F_p\, à p éléments, simplement en réduisant les équations pour V. De nouveau, pour presque tous les p, elle sera non-singulière. Nous définissons

Z_{V,Q}(s)\,

comme étant la série de Dirichlet de la variable complexe s, qui est le produit infini de fonctions zêta locales

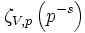\zeta_{V,p}\left(p^{-s}\right)\,.

Alors 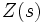Z(s)\,, selon notre définition, est bien définie seulement jusqu'à la multiplication par les fonctions rationnelles en un nombre fini de p^{-s}\,.

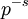Puisque l'indétermination est relativement anodine, et possède un prolongement analytique partout, il existe une signification dans laquelle les propriétés de Z(s) ne dépendent pas essentiellement d'elle. En particulier, tandis que la forme exacte de l'équation fonctionnelle pour 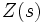Z(s)\,, se reflete dans une droite verticale dans le plan complexe, qui dépendra de manière finie de facteurs 'manquants', ce qui n'est pas le cas pour l'existence de quelques équations fonctionnelle de cette sorte.

Une définition plus raffinée est devenue possible avec le développement de la cohomologie étale; ceci explique de manière ordonnée que faire avec les facteurs de 'mauvaise réduction', manquants. Selon les principes généraux visibles dans la théorie de la ramification, les 'mauvais' nombres premiers portent une bonne information (théorie du conducteur). Ceux-ci se manifestent d'eux-mêmes dans la théorie étale par le critère de Ogg-Néron-Shafarevich pour la bonne réduction; expressément, il existe une bonne réduction, dans un sens défini, à tous les nombres premiers p pour lesquels la représentation de Galois ρ sur les groupes cohomologiques étales de V est non-ramifiée. Pour ceux-ci, la définition de fonction zêta locale peut être recouverte en termes de polynôme caractéristique de

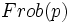\rho(Frob(p))\,

Frob(p)\, étant un élément de Frobenius pour p. Ce qui arrive au p ramifié est que ρ est non-trivial sur le groupe d'inertie I(p) pour p. À ces nombres premiers, la définition doit être 'corrigée', en prenant le plus grand quotient de la représentation ρ sur lequel le groupe d'inertie agit par la représentation triviale. Avec ce raffinement, la définition de Z(s) peut être améliorée successivement de 'presque tous' les p jusqu'à tous les p participant au produit eulérien. Les conséquences pour l'équation fonctionnelle ont été établies par Serre et Deligne à la fin des années 1960 ; l'équation fonctionnelle elle-même n'a pas été démontrée en général.

Référence

  • J.-P. Serre, Facteurs locaux des fonctions zêta des variétés algébriques (définitions et conjectures), 1969/1970, Sém. Delange-Pisot-Poitou, exposé 19


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction z%C3%AAta de Hasse-Weil ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction Zeta De Hasse-Weil de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Fonction zeta de Hasse-Weil — Fonction zêta de Hasse Weil En mathématiques, la fonction zêta de Hasse Weil attachée à une variété algébrique V définie sur un corps de nombres K est un des deux types les plus importants des fonctions L. De telles fonctions L sont appelées… …   Wikipédia en Français

  • Fonction zeta de hasse-weil — Fonction zêta de Hasse Weil En mathématiques, la fonction zêta de Hasse Weil attachée à une variété algébrique V définie sur un corps de nombres K est un des deux types les plus importants des fonctions L. De telles fonctions L sont appelées… …   Wikipédia en Français

  • Fonction zêta de Hasse-Weil — En mathématiques, la fonction zêta de Hasse Weil attachée à une variété algébrique V définie sur un corps de nombres K est un des deux types les plus importants des fonctions L. De telles fonctions L sont appelées globales , elles sont définies… …   Wikipédia en Français

  • Fonction Zeta Locale — Fonction zêta locale En mathématiques et dans la théorie des nombres, une fonction zêta locale est une fonction génératrice pour le nombre de solutions d un ensemble d équations définies sur un corps fini F, dans les extensions de corps de F. L… …   Wikipédia en Français

  • Fonction Zeta locale — Fonction zêta locale En mathématiques et dans la théorie des nombres, une fonction zêta locale est une fonction génératrice pour le nombre de solutions d un ensemble d équations définies sur un corps fini F, dans les extensions de corps de F. L… …   Wikipédia en Français

  • Fonction zeta locale — Fonction zêta locale En mathématiques et dans la théorie des nombres, une fonction zêta locale est une fonction génératrice pour le nombre de solutions d un ensemble d équations définies sur un corps fini F, dans les extensions de corps de F. L… …   Wikipédia en Français

  • Fonction Zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction zêta locale — En mathématiques et dans la théorie des nombres, une fonction zêta locale est une fonction génératrice pour le nombre de solutions d un ensemble d équations définies sur un corps fini F, dans les extensions de corps de F. L analogie avec la… …   Wikipédia en Français

  • Fonction zêta — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction zêta de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”