- Extension JPG
-
JPEG
Cet article concerne le format. Pour le groupe, voir Joint Photographic Experts Group.
Une photo de fleur compressée en JPEG, avec des compressions de plus en plus fortes, de gauche à droite.
La norme JPEG est une norme qui définit le format d'enregistrement et l'algorithme de décodage pour une représentation numérique compressée d'une image fixe.
Sommaire
Introduction au JPEG
JPEG est l’acronyme de Joint Photographic Experts Group. C’est un comité d’experts qui édite des normes de compression pour l’image fixe. La norme communément appelée JPEG, de son vrai nom ISO/IEC IS 10918-1 | ITU-T Recommendation T.81, est le résultat de l’évolution des travaux qui ont débuté dans les années 1978 à 1980 avec les premiers essais en laboratoire de compression d’images.
Le groupe JPEG qui a réuni une trentaine d’experts internationaux, a spécifié la norme en 1991. Mais la norme officielle et définitive n'a été adoptée qu'en 1992. Pratiquement, seule la partie concernant le codage arithmétique est brevetée, et par conséquent protégée par IBM, son concepteur.
JPEG normalise uniquement l’algorithme et le format de décodage. Le processus d'encodage est laissé libre à la compétition des industriels et universitaires, du moment que l’image produite est décodable par un décodeur standard. La norme propose un jeu de fichiers de tests appelés fichiers de conformance qui permettent de vérifier qu'un décodeur respecte bien la norme. Un décodeur est alors dit conforme s’il est capable de décoder tous les fichiers de conformance.
Le brevet de la norme JPEG a été déposé par l'entreprise Forgent[1], mais il a été remis en cause par le bureau américain des brevets (USPTO), qui l'a invalidé le 24 mai 2006 pour antériorité existante à la suite d'une plainte de la Public Patent Foundation qui considère ce brevet invalide[2]. Mais depuis le 27 septembre 2007, la société Global Patent Holdings, filiale d'Acacia Research Corporation, a à son tour revendiqué la paternité de ce format.
JPEG définit deux classes de processus de compression :
- avec pertes ou compression irréversible. C’est le JPEG « classique ». Il permet des taux de compression de 3 à 100.
- sans pertes ou compression réversible. Il n’y a pas de pertes d’information et il est donc possible de revenir aux valeurs originales de l’image. Les gains en termes de compression sont alors plus modestes, avec un taux de compression de l’ordre de 2. Cette partie fait l’objet d’une norme spécifique JPEG-LS.
La compression JPEG
Nous allons maintenant nous intéresser à l’algorithme.
On peut diviser la compression et la décompression JPEG en six étapes dont voici l’organigramme :
Figure 1 : Organigramme de compression.
Attention, quand on suit l'algorithme du bas, on n'aboutit pas à l'image brute, mais à une image restituée, qui n'est en aucun cas l'image brute. Entre l'image brute et l'image restituée, il y a des écarts, qui seront d'autant plus importants que l'opération de quantification a été forte.
Découpage en blocs
Le format JPEG, comme le font généralement les algorithmes de compression à perte, commence par découper l’image en blocs ou carreaux généralement carrés de 64 (8 x 8) ou 256 (16 x 16) pixels.
Transformation des couleurs
JPEG est capable de coder les couleurs sous n’importe quel format, toutefois les meilleurs taux de compression sont obtenus avec des codages de couleur de type luminance/chrominance tels que YUV, YCbCr car l’œil est assez sensible à la luminance mais peu à la chrominance.
Sous-échantillonnage
La façon la plus simple d’exploiter la faible sensibilité de l'œil à la chrominance est simplement de sous-échantillonner les signaux de chrominance. Généralement on utilise un sous-échantillonnage de type 2h1v ou 2h2v. Dans le premier cas (le plus utilisé) on a un sous-échantillonnage 2:1 horizontalement et 1:1 verticalement, dans le deuxième cas on a un sous-échantillonnage 2:1 horizontalement et verticalement. Ces sous-échantillonnages sont utilisés pour les chrominances, pour la luminance on n’utilise jamais de sous-échantillonnage.
Transformée DCT
La transformée DCT (Discrete Cosine Transform, en français transformée en cosinus discrète), est une transformation numérique qui est appliquée à chaque bloc et pour chaque « couleur ». Cette transformée est une variante de la transformée de Fourier. Cette méthode permet de décrire chaque bloc en une carte de fréquences et en amplitudes plutôt qu'en pixels et couleurs. La valeur d’une fréquence reflète l’importance et la rapidité d’un changement, tandis que la valeur d’une amplitude correspond à l’écart associé à chaque changement de couleur.
À chaque bloc de
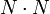pixels sont ainsi associées 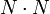fréquencesLa transformée DCT s’exprime mathématiquement par :
![\mathrm{DCT}(i, j)=\frac{2}{N}C(i)C(j)\sum_{x=0}^{N-1}\sum_{y=0}^{N-1}
\mathrm{pixel}(x, y) \cos\left[\frac{(2x+1)i\pi}{2N} \right] \cos\left[\frac{(2y+1)j\pi}{2N} \right]](/pictures/frwiki/53/57f7158d2cad9fe450827ef840d62630.png)
Équation 1 : Transformée DCT directe. Et la transformée DCT inverse s’exprime par :
![\mathrm{pixel}(x, y)=\frac{2}{N}\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}
C(i)C(j)\,\mathrm{ DCT}(i, j) \cos\left[\frac{(2x+1)i\pi}{2N} \right] \cos\left[\frac{(2y+1)j\pi}{2N} \right]](/pictures/frwiki/57/99476e8174245607be781a3c9d2af3b5.png)
Équation 2 : Transformée DCT inverse. Dans les deux cas, la constante
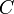vaut :![C(x)=\left\{\begin{matrix}\frac{1}{\sqrt{2}}&
\mathrm{pour}~ x = 0 \\[1ex] 1 & \mathrm{pour}~ x > 0 \end{matrix}\right.](/pictures/frwiki/54/66b0bae8dd1a26446f7698197df12b11.png)
Équation 3 : Définition de la constante C. Pour illustrer la compression a été repris un exemple complet provenant de « Digital Images Compression Techniques » de Majid Rabbani et Paul W. Jones.
Matrice (bloc de pixels) de base :
Équation 4 : Matrice d’origine. En effectuant la transformée DCT on obtient la matrice des fréquences suivante :
Équation 5 : Matrice transformée DCT. Remarques
Le calcul d’une DCT est complexe. C’est l’étape qui coûte le plus de temps et de ressources dans la compression et la décompression JPEG, mais c’est peut-être la plus importante car elle nous a permis de séparer les basses fréquences et les hautes fréquences présentes dans l’image.
La puissance de calcul disponible aujourd’hui, alliée à des algorithmes de type FFT très efficaces, permet de rendre le temps de calcul tout à fait acceptable pour l’utilisateur courant, voire imperceptible pour les machines les plus puissantes.
Quantification
La quantification est l’étape dans laquelle on perd réellement des informations (et donc de la qualité visuelle), mais c'est celle qui fait gagner beaucoup de place (contrairement à la DCT, qui ne compresse pas).
La DCT a retourné, pour chaque bloc, une matrice de 8x8 nombres (dans l’hypothèse que les blocs de l’image font 8x8 pixels). La quantification consiste à diviser cette matrice par une autre, appelée matrice de quantification, et qui contient 8x8 coefficients savamment choisis par le codeur.
Le but est ici d’atténuer les hautes fréquences, c’est-à-dire celles auxquelles l’œil humain est très peu sensible. Ces fréquences ont des amplitudes faibles, et elles sont encore plus atténuées par la quantification (les coefficients sont même ramenés à 0).
Voici le calcul permettant la quantification :
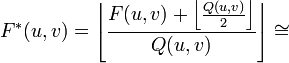entier le plus proche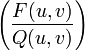 
Avec :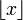 
entier directement inférieur à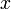 
Équation 6 : Calcul de la quantification. Et pour la quantification inverse :
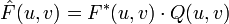
Équation 7 : Calcul de la quantification inverse. Comme le montre l’image ci-dessous la quantification ramène beaucoup de coefficients à 0 (surtout en bas à droite dans la matrice, là où sont les hautes fréquences). Seules quelques informations essentielles (coin en haut à gauche) sont gardées pour représenter le bloc.
L'intérêt est qu'au moment de coder le résultat dans le fichier, la longue suite de zéros nécessitera très peu de place !
Mais si la quantification est trop forte (= taux de compression trop élevé), il y aura trop peu de coefficients non nuls pour représenter fidèlement le bloc ; dès lors, à l’écran la division en blocs devient visible, et l'image apparaît « pixellisée ».
Dans notre exemple nous avons pris la matrice de quantification suivante :
Équation 8 : Matrice définissant le niveau de quantification. Ce qui donne comme matrice des fréquences quantifiée :
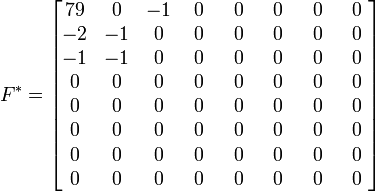
Équation 9 : Matrice quantifiée. Remarques
Codage, compression RLE et Huffman
Le codage s’effectue en zigzag comme le montre la figure suivante et se termine par un caractère de fin :
Figure 2 : Ordre de codage défini par la norme JPEG. Codage de notre exemple :
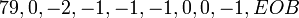.Ce résultat est ensuite compressé selon un algorithme RLE basé sur la valeur 0 (le codage RLE intervient uniquement sur cette dernière), puis un codage entropique de type Huffman ou arithmétique.
Avec le schéma de codage très simplifié suivant on remarque que le codage nous délivre deux tables (quatre pour une image couleur). Ces tables étant enregistrées dans le fichier final peuvent être choisies par le compresseur.
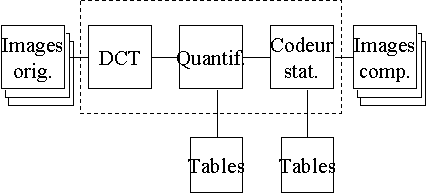
Figure 3 : Schéma de codage simplifié. Décompression JPEG
Les étapes de la décompression s’effectuent dans l’ordre inverse de la compression suivant les méthodes définies précédemment (en même temps que la compression).
Voici dans notre exemple le résultat de la décompression :
Équation 10 : Résultat de la décompression. Ainsi que la matrice d’erreur :
Équation 11 : Matrice des erreurs réalisées par les pertes. Remarques
Les erreurs sont au maximum de 5 et en moyenne 1,6 sur environ 150 ce qui nous donne une erreur moyenne d’environ 1 %, et tout cela pour un passage de 64 à 10 valeurs (avec le caractère de fin) ; à cela il faut rajouter la matrice de quantification, mais comme généralement on compresse de gros fichiers, elle n’influence que peu.
JPEG, codage sans pertes
Ici, la précision p des échantillons varie de 2 à 16 bits. À la place de la DCT, le codage utilise un prédicteur P à trois échantillons.
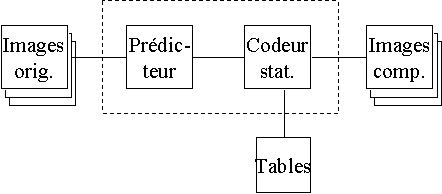
Figure 4 : Schéma de compression JPEG sans pertes. Voir aussi
Notes et références
Série JPEG Groupe JPEG JFIF JPEG-LS JPEG JPEG 2000 Compression par ondelettes 
Portail de l’informatique
t = (ti-tc)/ti, si ti et tc symbolisent respectivement les tailles initiale et après compression.Exemple : si la taille initiale est 4, et la taille après compression 1, le taux est égal à (4-1)/4 = 0,75 = 75%.
Catégorie : Imagerie numérique
Wikimedia Foundation. 2010.
