Espace de Hausdorff

Espace de Hausdorff

Espace séparé

En topologie et dans d'autres branches des mathématiques, un espace séparé ou espace de Hausdorff est un espace topologique dans lequel, pour deux points distincts x et y quelconques, il existe un voisinage de x et un voisinage de y disjoints. De tous les axiomes de séparation qui peuvent être demandés à un espace topologique, la condition séparé est un des plus fréquemment supposés et discutés.

Les espaces de Hausdorff doivent leur nom à Felix Hausdorff, mathématicien allemand qui fut l'un des fondateurs de la topologie. D'ailleurs, dans sa définition originale d'espace topologique, Hausdorff supposait cette condition réalisée.

Sommaire

Exemples et contre-exemples

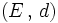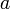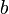Tout espace métrique est séparé. En effet soit (E\, ,\,d)\; un espace métrique, et soit a\; et b\; deux points distincts de 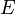E\;. Notons 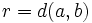r=d(a,b)\; alors la boule de centre 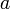a\; et de rayon 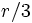r/3\; (resp. la boule de centre 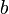b\; et de rayon 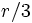r/3\;) est un voisinage de 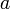a\; (resp. 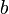b\;) et les deux boules ont une intersection nulle.

Pour un exemple d'espace non séparé, on peut regarder du côté de la topologie cofinie ou encore de la topologie de Zariski.

Propriété fondamentale

Dans un espace topologique séparé, une suite convergente a une limite unique.

Preuve

Supposons que 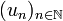(u_n)_{n\in{\mathbb N}} soit une suite convergeant vers les points x et y dans un espace topologique séparé.

Soit Vx un voisinage de x et Vy un voisinage de y.

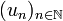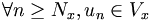(u_n)_{n\in{\mathbb N}} tend vers x donc il existe un entier Nx tel que \forall n \geq N_x, u_n \in V_x.

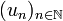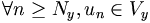(u_n)_{n\in{\mathbb N}} tend vers y donc il existe un entier Ny tel que \forall n \geq N_y, u_n \in V_y.

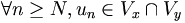Posons N = max(Nx,Ny). On a immédiatement \forall n \geq N, u_n \in V_x\cap V_y.

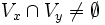Et donc V_x\cap V_y\neq\empty.

Autrement dit, un voisinage de x et un voisinage de y ont forcément des points en commun, ce qui dans un espace topologique séparé implique que x = y (contraposée de la définition de séparé).

Ainsi une suite convergente d'un espace topologique séparé ne peut converger vers deux limites distinctes. CQFD.

Propriétés voisines de la séparation

On trouvera dans l'article glossaire topologique plusieurs notions de séparation dans les espaces topologiques. La séparation de deux points distincts par deux voisinages disjoints y possède la classification T2.

La séparation T1

Une propriété de séparation plus faible est la propriété T1. Un espace T1 est tel que deux points distincts possèdent chacun un voisinage qui ne contient pas l'autre point. Un espace T2 est évidemment T1, mais la réciproque est fausse. Par exemple, un espace E infini dont les ouverts non vides sont les complémentaires des parties finies est T1 mais pas T2.

Dans un espace T1, les singletons sont des fermés. En effet soit a un point quelconque. Quel que soit x élément de l'espace topologique il existe un voisinage de x ne contenant pas a. L'union de tous ces voisinages quand x parcourt le complémentaire de a est un ouvert. Le complémentaire de a est donc un ouvert. Dans un tel ensemble, tout ensemble de cardinal fini est fermé.

Dans un espace T1, tout point est intersection de ses voisinages. Dans un espace T2, il suffit de prendre l'intersection des voisinages fermés.

La séparation T2 1/2

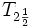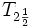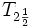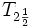Une propriété de séparation plus forte que la séparation T2 est la propriété T_{2 {1 \over 2}}. Dans un espace T_{2 {1 \over 2}}, deux points distincts admettent des voisinages dont les adhérences sont disjointes. Tout espace T_{2 {1 \over 2}} est un espace T2, mais la réciproque est fausse, comme le montre l'exemple suivant qui est T2 mais pas T_{2 {1 \over 2}}.

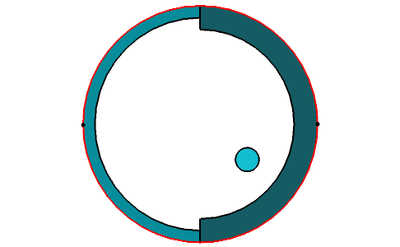
On considère l'ensemble E constitué de l'intérieur du disque de centre O de rayon 1 et des deux points (1,0) et (-1,0). Une base de voisinages d'un point intérieur au disque est formée des disques centrés en ce point. Une base de voisinages du point (1,0) est constituée de la réunion de ce point et d'une bande semi-circulaire adjacente à ce point et limitée par des segments [(0,1), (0,1-h)] et [(0,-1), (0,-1+h)]. De même pour (-1,0). Dans le dessin ci-dessous, on a représenté en couleur un voisinage d'un point intérieur au disque, et un voisinage de chacun des points (1,0) et (-1,0). Si ces deux derniers voisinages sont ouverts, ils sont disjoints, mais leurs adhérences s'intersectent selon une partie des segments communs qui les limitent. 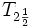E est donc séparé, mais il ne vérifie pas la propriété T_{2 {1 \over 2}}.

Espace topologique séparé

La séparation T4

Article détaillé : Espace normal.
Normal space.svg

La séparation T4 est une séparation plus forte que la précédente. Elle correspond à la notion d'espace normal. Un espace est dit normal s'il est séparé et si, pour tout couple de fermés disjoints E et F, il existe un couple d'ouverts disjoints U et V tel que U contienne E et V contienne F.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Espace s%C3%A9par%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace de Hausdorff de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • HAUSDORFF (F.) — HAUSDORFF FELIX (1868 1942) La renommée du mathématicien allemand Felix Hausdorff repose surtout sur son ouvrage Grundzüge der Mengenlehre (1814), qui en fit le fondateur de la topologie et de la théorie des espaces métriques. Né à Breslau dans… …   Encyclopédie Universelle

  • Espace Séparé — En topologie et dans d autres branches des mathématiques, un espace séparé ou espace de Hausdorff est un espace topologique dans lequel, pour deux points distincts x et y quelconques, il existe un voisinage de x et un voisinage de y disjoints. De …   Wikipédia en Français

  • Espace separe — Espace séparé En topologie et dans d autres branches des mathématiques, un espace séparé ou espace de Hausdorff est un espace topologique dans lequel, pour deux points distincts x et y quelconques, il existe un voisinage de x et un voisinage de y …   Wikipédia en Français

  • Espace séparé —  Ne pas confondre avec la structure d espace séparable. Deux points admettant des voisinages disjoints. Somm …   Wikipédia en Français

  • Espace Topologique — La topologie générale est une branche des mathématiques qui fournit un vocabulaire et un contexte général pour traiter des notions de limite, de continuité, dans le cadre d un continuum ou d un espace discret, voire fini. Dans ce contexte, les… …   Wikipédia en Français

  • Espace topologique — La topologie générale est une branche des mathématiques qui fournit un vocabulaire et un cadre général pour traiter des notions de limite, de continuité, et de voisinage. Les espaces topologiques forment le socle conceptuel permettant de définir… …   Wikipédia en Français

  • Espace de Hölder — Condition de Hölder En analyse, la continuité Höldérienne ou la condition de Hölder est une condition suffisante pour qu une application définie entre espaces métriques soit continue. Si (X,d) et (Y,d ) sont deux espaces métriques, une fonction… …   Wikipédia en Français

  • Espace compact — Compacité (mathématiques) Pour les articles homonymes, voir Compacité et Compact. En topologie de la droite réelle, la propriété de Borel Lebesgue est une propriété topologique remarquable des segments, basée sur la notion de recouvrement. Elle… …   Wikipédia en Français

  • Espace pointé — En topologie, un espace pointé est un espace topologique dont on spécifie un point particulier comme étant le point de base. Formellement, il s agit donc d un couple (E,x) pour lequel x est un élément de E. Une application pointée entre deux… …   Wikipédia en Français

  • Distance De Hausdorff — Felix Hausdorff (1868 1942) est le mathématicien à l origine de la distance portant maintenant son nom. En géométrie, la distance de Hausdorff est un outil topologique qui mesure l’éloignement de deux sous ensembles d’un espace …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”