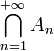- Espace de Baire
-
Théorème de Baire
Le théorème de Baire, dit aussi lemme de Baire, est un théorème de topologie dû au mathématicien René Baire. Un espace topologique est dit de Baire si toute intersection dénombrable d'ouverts denses est dense. De façon équivalente, un espace topologique est de Baire si une union dénombrable de fermés d'intérieur vide est d'intérieur vide.
Sommaire
Description
- Un espace topologique localement compact E est de Baire ;
- Un espace métrique complet (E,d) (notamment un espace de Banach) est de Baire ;
- Tout ouvert d'un espace de Baire est un espace de Baire.
DémonstrationDans ce qui suit, int(A) désigne l'intérieur d'une partie A de E.
1. Soit
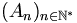une suite d'ouverts denses dans E localement compact. Soit V un ouvert quelconque (non vide); nous voulons montrer que :rencontre cet ouvert. Comme E est localement compact, on peut sans perte de généralité supposer que cet ouvert est relativement compact (ie d'adhérence compacte).
Puisque A1 est dense, il rencontre V : soit
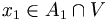. Ce dernier ensemble, intersection de deux ouverts, est ouvert. Il existe donc un voisinage compact 
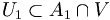de x1 (car il existe un système fondamental de voisinages compacts). Une fois U1 choisi, 
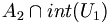est un ouvert non vide. Il existe donc un compact 
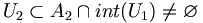.En itérant cette construction, on obtient une suite de compacts
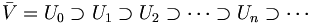avec 
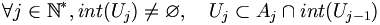.Or,
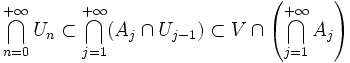et l'intersection des Un est non vide. En effet, les Uj sont des parties compactes de 
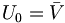; si leur intersection était vide, il en serait de même pour une certaine suite finie extraite (propriété de Borel-Lebesgue). Or, les Un sont une suite décroissante d'ouverts non vides donc cela est impossible. Finalement, 
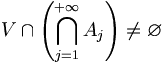, ce qui prouve le résultat.2. Dans le cas où E est un espace métrique complet, le raisonnement est analogue. Soit V une boule fermée centrée en
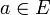et de rayon strictement positif. Il existe une suite de boules fermées de centre xn et de rayon inférieur à 
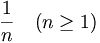telles que 
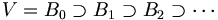avec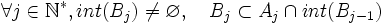 
. La suite des Bn étant décroissante, on a 
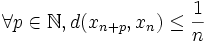. La suite 
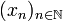est donc une suite de Cauchy : elle converge donc vers un élément x qui appartient à toutes les Bn et 
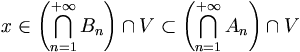, ce qui prouve le résultat.3. Soient O un ouvert d'un espace de Baire E et (Un) une suite d'ouverts de O denses dans O, autrement dit chaque Un est un ouvert de E, inclus dans O, et dont l'adhérence (dans E) contient O. Soit U l'intersection des Un, il s'agit de prouver que son adhérence contient O. Posons
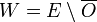et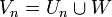 
. Alors les Vn sont des ouverts denses de E, donc leur intersection est dense, autrement dit l'adhérence de U contient 
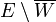. Or ce dernier ensemble contient O, ce qui conclut.Quelques applications
- Analyse fonctionnelle :
- Théorèmes de l'application ouverte, du graphe fermé, de l'isomorphisme de Banach ;
- Théorème de Banach-Steinhaus ;
- Théorème de la limite simple de Baire ;
- Théorème de Baire-Brenef ;
- L'ensemble des fonctions nulle part dérivables contient un Gδ dense pour la norme de la convergence uniforme dans l'ensemble des fonctions continues sur un intervalle I.
- Connexité du tipi de Cantor ;
- Théorème de superposition de Kolmogorov ;
- Caractérisation des polynômes réels[1],[2] : Si
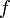est une fonction 
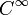telle que 
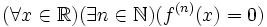, alors c'est un polynôme
On peut noter l'inversion de quantificateurs avec la caractérisation évidente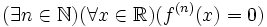
). Ici, 
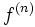désigne la dérivée n-ième de .
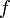Notes et références
- ↑ Carominas et Sunyer Balaguer, Revista Mat. Hisp.-Amer., 4, n°14, (1954), p.26-43
- ↑ H. D. Brunk and R. P. Boas, Amer. Math. Monthly, 66, n°7 (Aug. - Sep., 1959), p. 599
Liens externes
- Gilles Godefroy, texte sur le théorème
- BwataBaire, un wiki qui se propose de recenser diverses applications du lemme de Baire, et de réfléchir aux relations qu'il entretient avec des phénomènes similaires.
Théorèmes de l'analyse fonctionnelleThéorème d'Ascoli • Théorème de Baire • Théorème de Banach-Alaoglu • Théorème de Banach-Mazur • Théorème de Banach-Schauder • Théorème de Banach-Steinhaus • Théorème du graphe fermé • Théorème de Hahn-Banach • Théorème de Lax-Milgram
Portail des mathématiques
Catégories : Topologie générale | Théorème de mathématiques
Wikimedia Foundation. 2010.
