Fonction continue nulle part dérivable

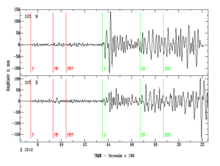Sismogramme du Tremblement de terre de 1906 à San Francisco, bien que continue, cette courbe n'est pas « arrondie ».

En mathématiques, une fonction continue nulle part dérivable est une fonction numérique qui est régulière du point de vue topologique (c'est-à-dire continue) mais ne l'est pas du tout du point de vue du calcul différentiel (c'est-à-dire qu'elle n'est dérivable en aucun point).

La continuité d'une fonction signifie que sa courbe représentative n'admet pas de « cassure ». La dérivabilité assure qu'elle est bien « arrondie ». Il est assez aisé de démontrer que toute fonction dérivable sur un intervalle est continue sur ce même intervalle. Les mathématiciens ont cru, jusqu'au XIX^e siècle que la réciproque était en partie vraie, que les points où une fonction continue n'est pas dérivable sont rares. Il n'en est rien. De nombreux contre-exemples furent découverts. Il fut même démontré que ces fonctions sont les plus nombreuses.

Depuis, l'étude de ces fonctions a montré qu'elles étaient importantes, non seulement du point de vue de la logique interne aux mathématiques, pour comprendre le concept de fonction, mais également pour fournir des modèles utiles aux autres sciences. Les fractales donnent également des exemples de courbes continues sans tangentes.

Histoire

Le concept même de fonction ne s'est clarifié qu'au XIX^e siècle, lorsqu'en 1837, Dirichlet pose une définition moderne du concept de fonction.

Définition — Une quantité y est une fonction (univoque) d'une quantité x, dans un intervalle donné quand à chaque valeur attribuée à x dans cet intervalle correspond une valeur unique et déterminée de y, sans rien spécifier sur la façon dont les diverses valeurs de y s'enchaînent les unes aux autres^[1].

À cette époque, les mathématiciens pensaient que toute fonction continue est dérivable, sauf éventuellement en quelques points particuliers, cette opinion n'étant pas contredite par leur pratique du calcul différentiel^[2]. Par exemple, André-Marie Ampère essaya de prouver que toute fonction est dérivable, sauf éventuellement en un nombre fini de points dans une publication de 1806^[3], sans cependant clarifier ce qu'il entendait par fonction^[4]. C'est pourquoi Bernhard Riemann étonna la communauté mathématique quand il exhiba, lors d'une conférence en 1861, un exemple de fonction qui est continue sur R mais dérivable seulement en de rares points^[4]. Cette fonction est définie par

$f(x)=\sum_{k=1}^{+\infty}\dfrac 1 k \sin (k^2 x)$

et n'est dérivable en x que lorsque x = $\dfrac{p\pi}{q}$ où p et q sont des entiers impairs.

En 1872, Karl Weierstrass fut le premier à publier non seulement une, mais tout une famille de fonctions continues et nulle part dérivables. Elles sont définies par

$f(x)=\sum_{k=0}^{+\infty}a^k \cos (b^k \pi x)$

où a et b sont des constantes réelles, a étant dans ]0,1[ et le produit ab strictement supérieur à 1 + ^3π⁄₂. Après cette découverte, des mathématiciens en trouvèrent d'autres^[4].

On alla même plus loin en prouvant que pour une fonction continue arbitraire, il existe une fonction continue partout et nulle part dérivable aussi proche d'elle que l'on désire. Cela signifie que ces fonctions particulières sont particulièrement nombreuses et forment un « gros » ensemble d'un point de vue topologique.

Perception

L'intérêt d'introduire ces fonctions, que l'on qualifie parfois de pathologiques, fut parfois rejeté par les mathématiciens. Citons par exemple Charles Hermite qui déclara en 1893 :

« Je me détourne avec effroi et horreur de cette plaie lamentable des fonctions continues qui n'ont point de dérivées^[5]. »

ou encore Henri Poincaré qui qualifie ces fonctions de « monstres »^{[Note 1]}.

Dans La Valeur de la Science, lorsqu'il faut donner des exemples pour lesquels l'intuition est mise en défaut en mathématiques, Poincaré donne ces fonctions en premier^{[Note 2]}.

La découverte de l'existence de ces fonctions a profondément modifié la vision qu'avaient les mathématiciens du concept de fonction et de celui de courbe. Les fonctions numériques réelles continues sont parfois présentées comme étant celles dont on peut tracer la courbe « sans lever le crayon »^[6]. Or, le graphe d'une fonction continue nulle part dérivable ne peut pas être tracé.

Ces fonctions sont encore considérées, au tournant des années 2000, comme contre-intuitives et comme un facteur bloquant pour l'apprentissage des mathématiques :

« Bien entendu, on sait maintenant qu’il existe des fonctions continues nulle part dérivables, mais, au niveau de l’enseignement secondaire, il n’y a aucun inconvénient à s'appuyer sur l’intuition contraire^[7]. »

Mandelbrot, l'inventeur des fractales, soutient au contraire que les courbes continues sans tangentes sont intuitives, mais reconnaît qu'il n'a trouvé, parmi ses prédécesseurs, que deux mathématiciens partageant cette opinion^[8].

Un exemple

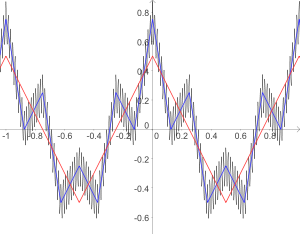
L'article fonction de Weierstrass présente un exemple historique d'une classe de fonctions continues partout nulle part dérivables. Nous allons en donner une autre.

On définit une fonction par

$g(x):=\begin{cases} 1+x & \text{si } x \in [-2,0] \\ 1-x & \text{si } x \in [0,2] \end{cases}$

Représentations graphiques de $\color{Red} f_1$ , $\color{Blue} f_2$ et $f_3\,$ dont $f\,$ est la limite

On peut la prolonger par périodicité sur tous les réels en posant pour tout $x$ réel

g (x + 4) = g (x)

On pose alors

$f(x):=\sum_{k=1}^{+\infty} \frac{1}{2^k} g(2^{2^k} x)$

Cette fonction est continue sur $\R$ , mais n'est dérivable en aucun point de $\R$ .

Principe de la construction. La fonction f est limite uniforme de fonctions $f n$ définies par :

$f_n(x):=\sum_{k=1}^{n} \frac{1}{2^k} g(2^{2^k} x)$

Ces fonctions $f n$ sont continues, affines par morceaux, mais leurs représentations graphiques sont formées de segments de droites dont les pentes sont de plus en plus raides.

Démonstration

Continuité

Par définition de $g$ , on a

$\sup_{x \in \R} \left| \frac{1}{2^k} g(2^{2^k} x) \right| = \frac{1}{2^k}$

Or la série géométrique

∑	2 ^{− k}
k

est convergente, si bien que la suite $(f n)$ converge normalement donc uniformément vers $f$ . Comme de plus $x \mapsto 2^{-k} g(2^{2^k} x)$ est continue sur $\R$ , il en est de même de $f n$ et de sa limite uniforme $f$ .

Dérivabilité

Soit $x \in \R$ . On va construire une suite de réels $(h n)$ convergeant vers 0 et telle que

$\lim_{n \to +\infty} \left|\frac{f(x+h_n) - f(x)}{h_n}\right| = + \infty$

ce qui assurera que $f$ n'est pas dérivable en $x$ .

Pour ce $x$ fixé et pour tout $n\in \N^*$ , on choisit $\varepsilon_n=\pm 1$ tel que $2^{2^n}x$ et $2^{2^n}x + \varepsilon_n$ soient dans le même intervalle de la forme $[2 N;2 N + 2]$ . On pose alors $h_n:= \varepsilon_n 2^{-2^n}$ .

Pour $k > n$ , on sait que $2^{2^k}h_n$ est un multiple de 4, et comme $g$ est de période 4, on a

$g(2^{2^k}(x+h_n))-g(2^{2^k}x)=0.$

Pour $k = n$ , on a

$g(2^{2^n}(x+h_n))-g(2^{2^n}x)|=|g(\varepsilon_n+2^{2^n}x)-g(2^{2^n}x)|=1.$

Pour $k < n$ , comme on sait, par construction de la fonction g que

$|g(b) - g(a)| \le |b-a|$

(la pente de la droite joignant deux points de

C g

est toujours comprise entre -1 et 1). On a en particulier

$|g(2^{2^k}(x+h_n))-g(2^{2^k}x)|\leq |2^{2^k}h_n| \leq 2^{2^{n-1}} 2^{-2^n} = 2^{-2^{n-1}}$

donc

$\left| \sum_{k=1}^{n-1}2^{-k}\left( g(2^{2^k}(x+h_n))-g(2^{2^k}x)\right) \right| \leq \left(\sum_{k=1}^{n-1}2^{-k}\right) 2^{-2^{n-1}}\leq 2^{-2^{n-1}}.$

On peut donc minorer le taux d'accroissement de $f$ en $x$ :

$\begin{align} \left| \frac{f(x+h_n)-f(x)}{h_n} \right| & = 2^{2^n} \left| \sum_{k=1}^{+\infty} 2^{-k}\left( g(2^{2^k}(x+h_n))-g(2^{2^k}x)\right) \right| \\ & = 2^{2^n} \left| \sum_{k=1}^{n} 2^{-k}\left( g(2^{2^k}(x+h_n))-g(2^{2^k}x)\right)\right| \\ & \geq 2^{2^n}\left( 2^{-n}- \left| \sum_{k=1}^{n-1} 2^{-k}\left( g(2^{2^k}(x+h_n))-g(2^{2^k}x)\right)\right| \right) \\ & \geq 2^{2^n} (2^{-n}- 2^{-2^{n-1}})= 2^{2^n-n} (1- 2^{n-2^{n-1}})\\ & \longrightarrow +\infty \text{ quand } n \to +\infty\end{align}$

Ceci montre que $f$ n'est pas dérivable en $x$ , or ce point est arbitraire, donc $f$ n'est dérivable en aucun point de $\R$ .

Densité

Théorème — Toute fonction continue sur $[0,1]$ est limite uniforme de fonctions continues nulle part dérivables sur $[0,1]$ .

Cela signifie que pour une fonction $f:[0,1] \rightarrow \R$ continue fixée et pour un $ε > 0$ arbitraire, il existe une fonction $g:[0,1] \rightarrow \R$ continue nulle part dérivable telle que

$\sup_{t \in [0,1]} |f(t) -g(t)| < \varepsilon.$

En d'autres termes, cela signifie que l'ensemble des fonctions continues et nulle part dérivable est dense dans l'ensemble des fonctions continues, pour la topologie de la convergence uniforme.

On peut énoncer un résultat analogue sur $\R$ : toute fonction continue sur $\R$ est localement limite uniforme de fonctions continues nulle part dérivables.

Démonstration

Soit $f:[0,1] \rightarrow \R$ continue. On a vu d'après la section précédente qu'il existe au moins une fonction $g:[0,1] \rightarrow \R$ continue partout nulle part dérivable. On sait alors que $f - g$ est une fonction continue de $[0,1]$ dans $\R$ , donc d'après le théorème de Stone-Weierstrass, il existe une suite $(P_n)_{n \in \N}$ de fonctions polynômiales de $[0,1]$ dans $\R$ telle que

$\sup_{t \in [0,1]} |(f-g)(t) -P_n(t)| \underset{n \rightarrow +\infty}{\longrightarrow} 0$

On a donc

$\sup_{t \in [0,1]} |f(t) -(g+P_n)(t)| \underset{n \rightarrow +\infty}{\longrightarrow} 0$

La fonction $f$ est donc limite uniforme sur $[0,1]$ de la fonction $g + P n$ , qui est continue comme somme de fonctions continues mais nulle part dérivable sur $[0,1]$ . En effet, soit $x \in [0,1]$ . On a

$\frac{(g+P_n)(x+h)-(g+P_n)(x)}{h} = \frac{g(x+h)-g(x)}{h}+\frac{P_n(x+h)-P_n(h)}{h}$

Or le premier terme de la somme diverge quand $h \rightarrow 0$ car $g$ n'est pas dérivable en $x$ , mais le second terme converge vers $P' n (x)$ , qui existe car une fonction polynômiale est infiniment dérivable.

On peut également fournir une démonstration non constructive (c'est-à-dire ne nécessitant pas d'exhiber un exemple de fonction continue nulle part dérivable) utilisant le lemme de Baire^[9].

Annexes

Bibliographie

Benoît Mandelbrot, Les objets fractals, 4^e édition, Flammarion, 1995 (ISBN 2080813013).
L'ouvrage de référence sur les fractales, leur découverte, leurs applications, par leur inventeur.
Henri Poincaré, Science et méthode, Flammarion, 1908 [lire en ligne]
(en) Johan Thim, Continuous Nowhere Differentiable Functions, 2003 [lire en ligne]
Une thèse. Étude complète de l'histoire des fonctions continues nulle part dérivables.

Notes

↑ La citation exacte est :

« La logique parfois engendre des monstres. On vit surgir toute une foule de fonctions bizarres qui semblaient s'efforcer de ressembler aussi peu que possible aux honnêtes fonctions qui servent à quelque chose. Plus de continuité, ou bien de la continuité, mais pas de dérivées[...] Autrefois, quand on inventait une fonction nouvelle, c'était en vue de quelque but pratique ; aujourd'hui, on les invente tout exprès pour mettre en défaut les raisonnements de nos pères, et on n'en tirera jamais que cela. »

Poincaré 1908, p. 132.
↑

« L’intuition ne peut nous donner la rigueur, ni même la certitude, on s’en est aperçu de plus en plus.
Citons quelques exemples. Nous savons qu’il existe des fonctions continues dépourvues de dérivées. Rien de plus choquant pour l’intuition que cette proposition qui nous est imposée par la logique. Nos pères n’auraient pas manqué de dire : « Il est évident que toute fonction continue a une dérivée, puisque toute courbe a une tangente. » »

Références

↑ Encyclopédie des sciences mathématiques pures et appliquées, Gauthier-Villard, 1909.
↑ Johan Thim 2003, p. 4.
↑ A. Ampère, Recherches sur quelques points de la théorie des fonctions dérivées qui conduisent à une nouvelle démonstration de la série de Taylor, et à l'expression finie de termes qu'on néglige lorsqu'on arrête cette série à un ordre quelconque, Journal de l'Ecole Polytechnique, No. 13, p. 148-191 (1806)
↑ ^{a, b et c} Johan Thim 2003.
↑ Lettre 374 d'Hermite à Stieljtes du 20 mai 1893, Correspondance d’Hermite et de Stieltjes, éd. B. Baillaud et H. Bourget. vol 2, Gauthier-Villars, 1905, p.317-319
↑ Par exemple le programme officiel de mathématiques de 2001 des classes de terminale S en France.
↑ Rapport d'étape sur la géométrie et son enseignement, Commission de réﬂexion sur l’enseignement des mathématiques, Janvier 2000, dit rapport Kahane, sur le site de la Société mathématique de France.
↑ Mandelbrot 1995, chap. II.
↑ Xavier Gourdon, Les maths en tête : analyse, éditions Ellipses

Liens externes

Portail de l'analyse

Catégories :

Analyse réelle
Fonction remarquable
Fractale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction continue nulle part dérivable de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Fonction continue dérivable nulle part — Fonction continue nulle part dérivable Sismogramme du Tremblement de terre de 1906 à San Francisco, bien que continue, cette courbe n est pas « arrondie ». En mathématiques, une fonction continue nulle part dérivable est une fonction… … Wikipédia en Français
Fonction continue — Continuité En mathématiques, la continuité est une propriété topologique d une fonction. En première approche, une fonction est continue si, à des variations infinitésimales de la variable x, correspondent des variations infinitésimales de la… … Wikipédia en Français
Fonction De Weierstrass — Représentation de la fonction de Weierstrass sur l intervalle [ 2,2]. La fonction a un comportement fractal : n importe quel zoom (par exemple le cercle rouge) ressemble au zoom total. La fonction de Weierstrass fut le premier exemple… … Wikipédia en Français
Fonction de weierstrass — Représentation de la fonction de Weierstrass sur l intervalle [ 2,2]. La fonction a un comportement fractal : n importe quel zoom (par exemple le cercle rouge) ressemble au zoom total. La fonction de Weierstrass fut le premier exemple… … Wikipédia en Français
Continue — Continuité En mathématiques, la continuité est une propriété topologique d une fonction. En première approche, une fonction est continue si, à des variations infinitésimales de la variable x, correspondent des variations infinitésimales de la… … Wikipédia en Français
Fonction de Weierstrass — Ne pas confondre avec les fonctions elliptiques de Weierstrass ou la fonction zêta de Weierstrass. Représentation de la fonction de Weierstrass sur l intervalle [ 2,2]. La fonction a un comporte … Wikipédia en Français
Fonction Convexe — En mathématiques, et plus particulièrement en analyse, une fonction convexe est une fonction numérique vérifiant une propriété de sous additivité vis à vis de la barycentration. Graphiquement, cela correspond à un graphe dont la « partie… … Wikipédia en Français
Fonction convexe — Fonction convexe. En mathématiques une fonction convexe est une fonction réelle d une variable réelle définie sur un intervalle et dont le graphe est « tourné vers le haut » : pour tous points A et B de ce graphe, le segment [AB]… … Wikipédia en Français
Fonction Entière — La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le plan complexe. C … Wikipédia en Français
Fonction entiere — Fonction entière La fonction associant à chaque nombre réel sa partie entière est traitée à l article Partie entière. Voir aussi la page Entier (homonymie). En analyse complexe, une fonction entière est une fonction holomorphe définie sur tout le … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction continue nulle part dérivable

Sommaire

Histoire

Perception

Un exemple

Densité

Annexes

Bibliographie

Notes

Références

Articles connexes

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Fonction continue nulle part dérivable

Sommaire

Histoire

Perception

Un exemple

Densité

Annexes

Bibliographie

Notes

Références

Articles connexes

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link