- Espace Pramétrique
-
Espace pramétrique
En mathématiques, un espace pramétrique est un espace topologique plus général que les espaces métriques, ne nécessitant ni symétrie, ni indiscernabilité, ni la validité de l'inégalité triangulaire. De tels espaces apparaîssent naturellement pour des applications entre espaces métriques.
Sommaire
Définition
Un espace pramétrique
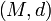 est la donnée d'un ensemble M et d'une fonction
est la donnée d'un ensemble M et d'une fonction 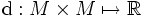 , appelée fonction pramétrique (ou pramétrique), qui vérifie les deux conditions suivantes :
, appelée fonction pramétrique (ou pramétrique), qui vérifie les deux conditions suivantes :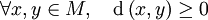 (positivité)
(positivité)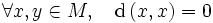
L'on peut avoir
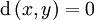 , alors que
, alors que 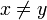 .
.Cas particuliers
Il existe peu de contraintes sur le choix d'une pramétrique. On peut ainsi imposer certaines propriétés :
- Si
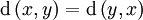 , la fonction pramétrique est dite « symétrique » ;
, la fonction pramétrique est dite « symétrique » ;
- Si de plus
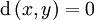 implique x = y, la fonction est dite « semimétrique » et engendre un espace semimétrique ;
implique x = y, la fonction est dite « semimétrique » et engendre un espace semimétrique ;
- Si de plus
- Si d vérifie l'inégalité triangulaire, elle est dite « hémimétrique » et engendre un espace hémimétrique ;
- Si de plus
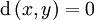 implique x = y, la fonction est dite « quasimétrique » et engendre un espace quasimétrique ;
implique x = y, la fonction est dite « quasimétrique » et engendre un espace quasimétrique ; - Si de plus d est symétrique, alors est est dite « pseudométrique » et engendre un espace pseudométrique ;
- Si de plus
Le cas où d vérifie ces trois propriétés est celui d'une métrique et la fonction d engendre un espace métrique.
Exemples
Soit
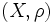 un espace métrique et
un espace métrique et 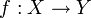 une application, alors la fonction :
une application, alors la fonction :est une pramétrique symétrique.
La fonction définie par :
est une pramétrique non-symétrique. Elle engendre la ligne de Sorgenfrey.
L'ensemble
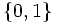 muni de la pramétrique :
muni de la pramétrique :- d (0,1) = 1 ;
- d (1, 0) = 0 ;
engendre pour cet ensemble une topologie connectée, qui en fait un espace de Sierpiński.
Propriétés topologiques
Au sens d'une pramétrique, une boule est définie par :
La particularité des espaces pramétriques est qu'une telle boule peut ne pas être un ouvert, et l'ensemble des boules peut ne pas constituer une base pour la topologie d'un tel espace. Il faut plutôt travailler avec l'ensemble des ouverts :
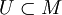 est un ouvert si et seulement si :
est un ouvert si et seulement si :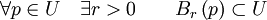 .
.
Par ailleurs, l'intérieur de la boule de centre p peut ne pas contenir p — l'intérieur peut même se restreindre à l'ensemble vide. Un autre aspect inhabituel de ces espaces est qu'un point situé dans un fermé[1] peut avoir une distance à ce fermé non-nulle :
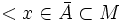 peut ne pas impliquer
peut ne pas impliquer 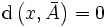
L'ensemble des points situés à une distance nulle d'un ensemble constitue une fermeture appelée prafermeture :
est une prafermeture sur X.
Une propriété intéressante des espaces pramétriques est qu'un espace topologique dont la topologie est engendrée par une pramétrique est un espace séquentiel.Notes et références
- ↑ Un ensemble
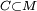 est dit fermé si et seulement si, pour tout
est dit fermé si et seulement si, pour tout 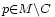 ,
, 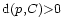 .
.
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Prametric space ».
Bibliographie
- (en)/(ru) A.V. Arkhangelskii, L.S. Pontryagin : General Topology I, (1990) Springer-Verlag, Berlin. (ISBN 3-540-18178-4)
- Portail des mathématiques
Catégorie : Topologie
Wikimedia Foundation. 2010.

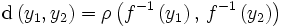
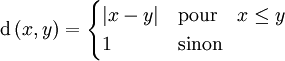
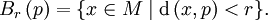
![[A]_p= \{ x \in X : \mathrm d \left(x,A \right)=0 \} \,](/pictures/frwiki/98/b693ab76769670d2761cb5ce5dbb4d74.png)