Hémimétrique
- Hémimétrique
-
Espace hémimétrique
En mathématiques, un espace hémimétrique est un cas particulier d'espace pramétrique, à qui l'on impose de vérifier l'inégalité triangulaire.
Définition
Un espace hémimétrique (M, d) est la donnée d'un ensemble M et d'une fonction 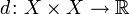 appelée fonction hémimétrique (ou hémimétrique), qui vérifie :
appelée fonction hémimétrique (ou hémimétrique), qui vérifie :
Cas particuliers
- En imposant à la fonction d d'être symétrique, on en fait une fonction pseudométrique, qui engendre un espace pseudométrique.
- Une hémimétrique qui distingue deux points est appelée quasimétrique, et engendre un espace quasimétrique.
- Une hémimétrique qui vérifie à la fois ces deux propriétés est une métrique, qui engendre un espace métrique.
Propriétés topologiques
Une hémimétrique induit une topologie sur M, une base des ouverts de M étant donnée par l'ensemble :
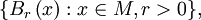
avec 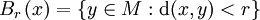 la boule ouverte de rayon r centrée en x.
la boule ouverte de rayon r centrée en x.
Références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Hemimetric space ».
 Portail des mathématiques
Portail des mathématiques
Catégories : Topologie | Espace métrique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Hémimétrique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Espace Hémimétrique — En mathématiques, un espace hémimétrique est un cas particulier d espace pramétrique, à qui l on impose de vérifier l inégalité triangulaire. Sommaire 1 Définition 2 Cas particuliers 3 Propriétés topologiques … Wikipédia en Français
Espace hemimetrique — Espace hémimétrique En mathématiques, un espace hémimétrique est un cas particulier d espace pramétrique, à qui l on impose de vérifier l inégalité triangulaire. Sommaire 1 Définition 2 Cas particuliers 3 Propriétés topologiques … Wikipédia en Français
Espace hémimétrique — En mathématiques, les notions d espace hémimétrique et de fonction hémimétrique sont la généralisation de celles d espace pseudométrique et d écart, en n imposant pas que la fonction soit symétrique. Sommaire 1 Définition 2 Cas particuliers 3… … Wikipédia en Français
Espace Pramétrique — En mathématiques, un espace pramétrique est un espace topologique plus général que les espaces métriques, ne nécessitant ni symétrie, ni indiscernabilité, ni la validité de l inégalité triangulaire. De tels espaces apparaîssent naturellement pour … Wikipédia en Français
Espace prametrique — Espace pramétrique En mathématiques, un espace pramétrique est un espace topologique plus général que les espaces métriques, ne nécessitant ni symétrie, ni indiscernabilité, ni la validité de l inégalité triangulaire. De tels espaces apparaîssent … Wikipédia en Français
Pramétrique — Espace pramétrique En mathématiques, un espace pramétrique est un espace topologique plus général que les espaces métriques, ne nécessitant ni symétrie, ni indiscernabilité, ni la validité de l inégalité triangulaire. De tels espaces apparaîssent … Wikipédia en Français
Espace Pseudométrique — En mathématiques, un espace pseudométrique est un cas particulier d espace hémimétrique vérifiant une relation de symétrie, qui généralise ainsi la notion d espace métrique. Lorsqu une topologie est générée par une famille de pseudométriques, l… … Wikipédia en Français
Espace Quasimétrique — En mathématiques, un espace quasimétrique est un cas particulier d espace hémimétrique, qui généralise ainsi la notion d espace métrique ne nécessitant pas la condition de symétrie. De tels espaces apparaissent parfois en théorie des graphes.… … Wikipédia en Français
Espace pseudometrique — Espace pseudométrique En mathématiques, un espace pseudométrique est un cas particulier d espace hémimétrique vérifiant une relation de symétrie, qui généralise ainsi la notion d espace métrique. Lorsqu une topologie est générée par une famille… … Wikipédia en Français
Espace quasimetrique — Espace quasimétrique En mathématiques, un espace quasimétrique est un cas particulier d espace hémimétrique, qui généralise ainsi la notion d espace métrique ne nécessitant pas la condition de symétrie. De tels espaces apparaissent parfois en… … Wikipédia en Français
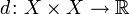 appelée fonction hémimétrique (ou hémimétrique), qui vérifie :
appelée fonction hémimétrique (ou hémimétrique), qui vérifie : (positivité) ;
(positivité) ;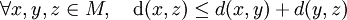 (inégalité triangulaire) ;
(inégalité triangulaire) ;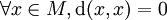 .
.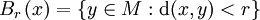 la boule ouverte de rayon r centrée en x.
la boule ouverte de rayon r centrée en x.