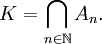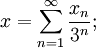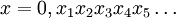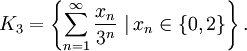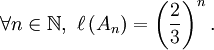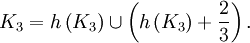- Ensemble triadique de Cantor
-
Ensemble de Cantor
En mathématiques, l'ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous-ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor.
Il s'agit d'un ensemble fermé du segment [0,1], d'intérieur vide. Il sert d'exemple pour montrer qu'il existe des ensembles infinis non dénombrables mais négligeables au sens de la mesure de Lebesgue. C'est aussi le premier exemple de fractale (bien que le terme ne soit apparu qu'un siècle plus tard), et il possède une dimension non-entière (voir plus bas).
Il admet enfin une interprétation en termes de développement des réels en base 3. Pour cette raison, il est souvent noté K3.
On le construit de manière itérative à partir du segment [0,1] en enlevant le tiers central ; puis on réitère l'opération sur les deux segments restants, et ainsi de suite. On peut voir les six premières itérations du procédé sur le schéma suivant :

Sommaire
Construction
Construction itérative
On dénote par
 l'opérateur « enlever le tiers central » :
l'opérateur « enlever le tiers central » :On note A0 = [0,1] et on définit par récurrence une suite de parties de [0,1] par la relation :
On a :
![A_3 = \left[0,\frac{1}{27}\right] \cup \left[\frac{2}{27},\frac{1}{9}\right] \cup \left[\frac{2}{9},\frac{7}{27}\right] \cup \left[\frac{8}{27},\frac{1}{3}\right] \cup \left[\frac{2}{3},\frac{19}{27}\right] \cup \left[\frac{20}{27},\frac{7}{9}\right] \cup \left[\frac{8}{9},\frac{25}{27}\right] \cup \left[\frac{26}{27},1\right].](/pictures/frwiki/56/83edc64bf4203eea5ddcecde5e52b0d9.png)
Alors l'ensemble de Cantor K3 est « la limite » de An quand n tend vers
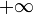 :
:Écriture en base 3
On peut aussi définir l'ensemble de Cantor via l'écriture en base 3. Tout réel
![x \in [0,1]](/pictures/frwiki/99/c628ba2b1047de93f66cb815d986e107.png) s'écrit de manière :
s'écrit de manière :avec
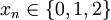 . On écrit alors
. On écrit alorsCette écriture est unique à ceci près : on peut remplacer
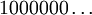 par
par 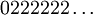 (et
(et 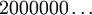 par
par 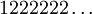 ) à la fin d'une écriture. Si on choisit de faire cette transformation on peut alors définir K3 par :
) à la fin d'une écriture. Si on choisit de faire cette transformation on peut alors définir K3 par :- L'ensemble de Cantor est formé des réels de [0,1] ayant une écriture en base 3 ne contenant que des 0 et des 2.
C'est-à-dire
Note : donc 1/3 est dans cet ensemble, puisqu'il admet les deux écritures 0,1000… et 0,02222… en base 3. 2/3 également (0,2000… ou 0,12222…). Remarquez que parmi les nombres admettant un développement propre et un développement impropre, il n'en existe aucun dont les deux écritures vérifient la propriété demandée.
Propriétés
L'ensemble de Cantor a de nombreuses propriétés particulières.
Mesure
L'ensemble de Cantor est de mesure nulle, c'est-à-dire négligeable au sens de la mesure de Lebesgue.
En effet en notant
 la mesure de Lebesgue sur
la mesure de Lebesgue sur  , on a :
, on a :![\ell \left( [0,1] \right) = 1](/pictures/frwiki/99/ca8b11a47879535bf014a8a342f4da1b.png) ;
;- pour une réunion An d'intervalles :
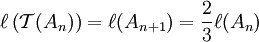 ;
;
où
 est l'opérateur « ablation du tiers central » (voir premier paragraphe).
est l'opérateur « ablation du tiers central » (voir premier paragraphe).On en déduit que pour les étapes de la construction itérative ci-dessus :
Et comme l'ensemble de Cantor est inclus dans tous les An :
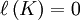 .
.L'ensemble de Cantor est donc « petit » au sens de la mesure de Lebesgue.
Non-dénombrabilité
Cependant l'ensemble de Cantor n'est pas dénombrable ; il a la puissance du continu (voir Infini).
En effet, on peut montrer que les ensembles K3 et [0,1] sont équipotents.
Pour cela on associe à tout élément
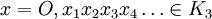 écrit en base 3, l'élément
écrit en base 3, l'élément ![f(x)=0,x'_1 x'_2 x'_3 x'_4 \ldots \in [0,1]](/pictures/frwiki/49/19d19b681e3fb7b504cd089840eb2ee8.png) écrit en base 2, avec :
écrit en base 2, avec :- x'i = 0 si xi = 0 ;
- x'i = 1 si xi = 2.
Par exemple l'élément
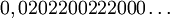 de l'ensemble de Cantor correspondra à l'élément
de l'ensemble de Cantor correspondra à l'élément  du segment unité [0,1].
du segment unité [0,1].Il est facile de voir que cette application est surjective mais non injective (l'élément 0,1 étant l'image de
 comme de 0,2). De l'existence d'une surjection de K3 dans [0,1], par l'axiome du choix, on déduit l'existence d'une injection de [0,1] dans K3, et comme l'application identité induit clairement une injection de K3 dans [0,1], alors d'après le théorème de Cantor-Bernstein, on en déduit que K3 et [0,1] sont équipotents. Donc l'ensemble de Cantor est aussi en bijection avec
comme de 0,2). De l'existence d'une surjection de K3 dans [0,1], par l'axiome du choix, on déduit l'existence d'une injection de [0,1] dans K3, et comme l'application identité induit clairement une injection de K3 dans [0,1], alors d'après le théorème de Cantor-Bernstein, on en déduit que K3 et [0,1] sont équipotents. Donc l'ensemble de Cantor est aussi en bijection avec  , il a la puissance du continu.
, il a la puissance du continu.On peut aussi utiliser l'écriture en base 3. Celle-ci montre que K3 est équipotent à
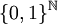 .
.Ainsi l'ensemble de Cantor est « grand » au sens de la théorie des ensembles.
Propriétés topologiques
- L'ensemble de Cantor est compact, et n'a que des points d'accumulation. On dit que c'est un ensemble parfait. Par ailleurs, il est d'intérieur vide,
DémonstrationSoit P un point de K3, et soit une boule ouverte (intervalle ouvert) centrée en P. Cet ouvert contient nécessairement un réel dont le développement en base 3 contient le chiffre 1, qui n'est pas élément de K3. Donc P n'est pas intérieur à K3. Par ailleurs, dans ce même intervalle, il existe toujours un réel dont le développement en base 3 s'écrit uniquement avec des 0 ou des 2. Donc P n'est pas un point isolé.
- L'ensemble de Cantor est également totalement discontinu c'est-à-dire que chaque singleton est sa propre composante connexe, et homéomorphe à l'espace topologique
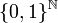 .
.
- Enfin l'ensemble de Cantor est « universel dans la catégorie des espaces métriques compacts», autrement dit tout espace métrique compact est l'image de l'ensemble de Cantor par une application continue. Cette affirmation a des répercussions importantes en analyse fonctionnelle.
Auto-similarité
L'image de l'ensemble de Cantor par l'homothétie h de centre 0 et de rapport 1/3 est elle-même une partie de l'ensemble de Cantor. Plus précisément
Ainsi, K3 est la réunion disjointe de deux parties qui lui sont homothétiques. C'est une manifestation de ce qu'on appelle l'auto-similarité, qui est l'une des propriétés de base des fractales.
Dimension
En conséquence de ce qui précède, on peut calculer la dimension de Minkowski ; elle vaut log(2)/log(3), nombre réel compris entre 0 et 1. On dit parfois qu'il est fractionnaire car il s'agit d'une fraction de logarithmes ; il faut bien comprendre que cela ne signifie pas qu'il s'agit d'un nombre rationnel, il ne l'est pas. Dans cette formule, peut importe qu'on interprète log comme logarithme naturel ou logarithme décimal, la fraction évite que le résultat diffère. On peut aussi écrire que la dimension vaut log3(2) (logarithme de 2 en base 3).
En fait, cette valeur est également la dimension de Hausdorff de l'ensemble. D'ailleurs à l'époque où ces dimensions ont été calculées, il n'était pas évident que les deux dimensions sont différentes pour certains ensembles.
On peut donc dire que l'ensemble de Cantor est de dimension log(2)/log(3) sans se soucier de la dimension utilisée.
Variante
Une autre version de l'ensemble de Cantor est l'ensemble de Cantor "quatre coins". Il est construit sur le même principe général, mais basé sur un carré : on considère un carré que l'on découpe en 16 carrés de même taille, et on supprime tous les carrés n'étant pas dans un coin du carré de départ. L'ensemble est construit de façon itérative en répétant cette action sur les nouveaux carrés.
Voir aussi
- Portail des mathématiques
Catégories : Théorie de la mesure | Fractale | Espace topologique remarquable | Georg Cantor
Wikimedia Foundation. 2010.

![\mathcal{T} : I \rightarrow I_0 \cup I_1 \ ; \ [a,b] \mapsto \left[a,a+\frac{b-a}{3}\right] \cup \left[b- \frac{b-a}{3},b\right].](/pictures/frwiki/57/9d2eccc48b7936e07ccd7515045747a0.png)
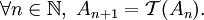
![A_1 = \left[0,\frac{1}{3}\right] \cup \left[\frac{2}{3},1\right];](/pictures/frwiki/48/0adedfa7e9f4ea3047a129ea092a4fae.png)
![A_2 = \left[0,\frac{1}{9}\right] \cup \left[\frac{2}{9},\frac{1}{3}\right] \cup \left[\frac{2}{3},\frac{7}{9}\right] \cup \left[\frac{8}{9},1\right];](/pictures/frwiki/98/b7d75520789366adc08dafc57209650a.png)