Ensemble Parfait

Ensemble Parfait

Ensemble parfait

Dans un espace topologique, un ensemble parfait est une partie fermée sans point isolé, ou de façon équivalente, une partie égale à l'ensemble de ses points d'accumulation.

Exemples

Dans \mathbb R, un segment [a,b] est un exemple trivial d'ensemble parfait.


Un exemple moins évident est constitué par l'ensemble de Cantor. Cet ensemble est totalement discontinu et homéomorphe à l'espace produit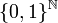 \{0,1\}^{\mathbb N} muni de la topologie produit. Plus généralement, l'espace {0,1}I est parfait lorsque I est un ensemble infini. 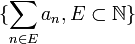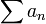Un exemple[1] d'ensemble parfait dans le plan, homéomorphe également à l'ensemble de Cantor, est donné par l'ensemble \{ \sum_{n \in E} a_n, E \subset \mathbb N\} où \sum a_n est une série absolument convergente de complexes telle que, pour tout N,

∑ | an | < | aN |
n > N

.


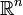On peut engendrer des ensembles parfaits de la façon suivante. Si P0 est une partie bornée de \mathbb R ou de \mathbb R^n, on définit le dérivéP' = P1 de P0 comme l'ensemble des points d'accumulation de P0. Pour tout ordinal α, on pose Pα + 1 = (Pα)', et, si α est un ordinal limite, 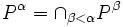P^{\alpha} = \cap_{\beta<\alpha} P^{\beta}. Si Ω désigne le premier ordinal non dénombrable, on montre que :

  • Ou bien 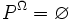P^{\Omega} = \varnothing. On dit que P0 est réductible.
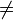
  • Ou bien PΩ 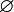\neq \varnothing et dans ce cas, c'est un ensemble parfait. P0 est la réunion de cet ensemble parfait et d'un ensemble dénombrable.

Notes et références

  1. ↑ Jean-Marie Arnaudiès, L'intégrale de Lebsegue sur la droite, Vuibert (1997), p18-20
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Ensemble parfait ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Ensemble Parfait de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Ensemble parfait — Dans un espace topologique, un ensemble parfait est une partie fermée sans point isolé, ou de façon équivalente, une partie égale à l ensemble de ses points d accumulation. Exemples Dans , un segment [a,b] est un exemple trivial d ensemble… …   Wikipédia en Français

  • Avec un ensemble parfait — ● Avec un ensemble parfait se dit lorsque plusieurs personnes commettent quelque chose visiblement d un commun accord ou avec une coïncidence étonnante …   Encyclopédie Universelle

  • parfait — parfait, aite [ parfɛ, ɛt ] adj. et n. • XIIe; parfit XIe; perfectus Xe; p. p. du v. parfaire, d apr. lat. perfectus I ♦ Qui est au plus haut, dans l échelle des valeurs. 1 ♦ Tel qu on ne puisse rien concevoir de meilleur. ⇒ …   Encyclopédie Universelle

  • Ensemble De Cantor — En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor. Il s agit d un ensemble fermé du segment… …   Wikipédia en Français

  • Ensemble de cantor — En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor. Il s agit d un ensemble fermé du segment… …   Wikipédia en Français

  • Ensemble triadique de Cantor — Ensemble de Cantor En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor. Il s agit d un ensemble …   Wikipédia en Français

  • ensemble — 1. ensemble [ ɑ̃sɑ̃bl ] adv. • fin XIe; lat. pop. insimul 1 ♦ L un avec l autre, les uns avec les autres. ⇒ collectivement, conjointement; co , con , syn (cf. En commun, de concert, de conserve). Plusieurs personnes ensemble. ⇒ réuni. Venez tous… …   Encyclopédie Universelle

  • Parfait — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Parfait est un nom propre ou plus souvent un adjectif ou un nom commun qui peut désigner : Adjectif une qualité de perfection, en quoi il n y a rien… …   Wikipédia en Français

  • Ensemble de Cantor — En mathématiques, l ensemble de Cantor (ou ensemble triadique de Cantor, ou poussière de Cantor) est un sous ensemble remarquable de la droite réelle construit par le mathématicien allemand Georg Cantor[1]. Il s agit d un sous ensemble fermé de l …   Wikipédia en Français

  • Ensemble réel — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”