- Surjective
-
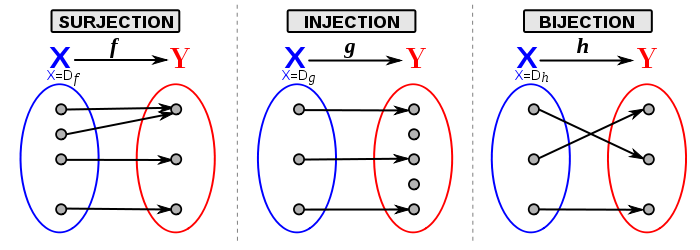
Surjection
Une surjection est une application surjective. Une application est surjective si et seulement si tout élément de son ensemble d'arrivée a au moins un antécédent, c'est-à-dire est image d'au moins un élément de son ensemble de départ, ou encore si tout élément de son ensemble d'arrivée fait partie de son ensemble image, donc si son ensemble d'arrivée se confond avec son ensemble image.
On peut remarquer que, dans cette définition, on n'impose pas de condition aux éléments de l'ensemble de départ. La définition de la surjectivité peut ainsi être étendue sans problème aux fonctions (et même aux correspondances), mais une fonction surjective n'est une surjection que si c'est une application, c'est-à-dire si elle est définie en tout point de son ensemble de départ.
Lorsque
 est une surjection dont l'ensemble de départ est
est une surjection dont l'ensemble de départ est 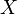 et dont l'ensemble d'arrivée est
et dont l'ensemble d'arrivée est 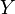 , on parle souvent de surjection de
, on parle souvent de surjection de 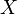 sur
sur 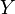 au lieu d'application de
au lieu d'application de 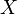 dans
dans 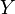 .
.Quand X et Y sont tous les deux égaux à la droite réelle
 , alors une fonction surjective
, alors une fonction surjective 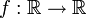 a un graphe qui intercepte toute droite horizontale.
a un graphe qui intercepte toute droite horizontale.Si une surjection est aussi une injection, alors on l'appelle une bijection. En fait une bijection est une surjection injective, ou une injection surjective.
Sommaire
Définition formelle
Soit f une application de X dans Y. L'application f est dite surjective si et seulement si tout élément de l'ensemble d'arrivée Y a au moins un antécédent par f, c'est-à-dire si :
C'est-à-dire : pour tout élément y de Y, il existe au moins un élément x de X tel que f(x) = y.
Définition équivalente : f est surjective si et seulement si son ensemble image se confond avec son ensemble d'arrivée.
Exemples
Exemple concret
On considère le cas d'une station de vacances où un groupe de touristes doit être logé dans un hôtel. Chaque façon de répartir ces touristes dans les chambres de l'hôtel peut être représentée par une application de l'ensemble des touristes, X, vers l'ensemble des chambres ,Y, (à chaque touriste est associée une chambre).
- Les touristes souhaitent que l'application soit injective, c'est-à-dire que chacun d'entre eux ait une chambre individuelle. Cela n'est possible que si le nombre de touristes ne dépasse pas le nombre de chambres.
- L'hôtelier souhaite que l'application soit surjective, c'est-à-dire que chaque chambre soit occupée. Cela n'est possible que s'il y a au moins autant de touristes que de chambres.
- Ces desiderata ne sont compatibles que si le nombre de touristes est égal au nombre de chambres. Dans ce cas, il sera possible de répartir les touristes de telle sorte qu'il y en ait un seul par chambre, et que toutes les chambres soient occupées : l'application sera alors à la fois injective et surjective ; on dira qu'elle est bijective.
rem: ici X représente l'ensemble des touristes et Y celui des chambres de l'hôtel
Exemples et contre-exemples dans les fonctions réelles
La fonction définie par
n'est pas surjective, car certains réels ne possèdent pas d'antécédent. Par exemple, il n'y a pas de réel x tel que f(x) = − 4,. Mais, si on change la définition de f en donnant comme ensemble d'arrivée R+, alors elle le devient car chaque élément y de l'ensemble d'arrivée possède au moins un antécédent, : 0 possède exactement un antécédent ,0, tous les autres réels y strictement positifs en possèdent deux
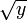 et
et 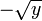 .
.La fonction définie par
est surjective, puisque pour tout réel arbitraire y, il existe des solutions à l'équation y = 2x + 1 d'inconnue x; une solution est x = (y − 1)/2.
La fonction définie par
n'est pas surjective car les réels strictement plus grands que 1 ou strictement plus petits que -1 n'ont pas d'antécédent.
Mais la fonction définie par
qui possède la même expression que g, mais avec un ensemble d'arrivée qui a été restreint à l'ensemble des nombres réels compris entre -1 et 1, est surjective. En effet, pour tout réel arbitraire y de l'intervalle [-1, 1], il existe des solutions à l'équation y = cos xd'inconnue x : ce sont les réels
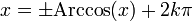 pour tout entier relatif k
pour tout entier relatif kSur ces quelques exemples, on voit qu'il est toujours possible de transformer une fonction non surjective en fonction surjective à condition de réduire la taille de son ensemble d'arrivée.
Propriétés
Réduction de l'ensemble d'arrivée
Si f est une fonction de X dans Y , si Df est l'ensemble de définition de f et si on note Y' l'image de Df par f alors l'application
- :
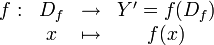
- est une surjection.
En d'autres termes, soient :
- f une fonction de E dans F,
- Df son ensemble de définition ( c'est-à-dire l'ensemble des antécédents des éléments de F par f )
- et Imf son ensemble image ( c'est-à-dire l'ensemble des images des éléments de E par f ).
- Note : Imf est aussi l'ensemble des images des éléments de Df par f, ou Imf ( Df ) = Imf.
Alors :
- si f est restreinte à Df, c'est-à-dire si on remplace son ensemble de départ par son ensemble de définition, elle devient une fonction applicative, c'est-à-dire une application;
- si f est corestreinte à Imf, c'est-à-dire si on remplace son ensemble d'arrivée par son ensemble image, elle devient surjective.
- si on combine les deux restrictions, c'est-à-dire si f est restreinte à Df et corestreinte à Imf, elle devient une application surjective, c'est-à-dire une surjection.
En résumé, le point important est que si on réduit l'ensemble d'arrivée d'une application à son ensemble image, elle devient une surjection. Il s'agit de l'action duale de la réduction de l'ensemble de départ d'une fonction à son ensemble de définition, cette dernière devenant ainsi une application.
Réciproque partielle
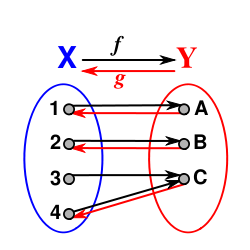
- Une fonction f de X dans Y est surjective si et seulement si il existe une fonction g de Y dans X telle que f
 g soit égale à l'application identité sur Y. g peut être considérée comme une réciproque partielle de f.
g soit égale à l'application identité sur Y. g peut être considérée comme une réciproque partielle de f.
- Cette propriété s'appuie sur le fait que l'on peut toujours remonter les flèches de Y vers X . Elle est toujours vraie si Y est fini. Dans le cas contraire, il est parfois nécessaire de faire appel à l'axiome du choix.
Théorème — Si la fonction f de X dans Y est surjective et si B est un sous-ensemble de Y, alors f ( f −1( B )) = B.
Ainsi, on remarque que B peut se retrouver à partir de l'image directe de f −1( B )
DémonstrationSoit f: X → Y une application surjective.
Soit B un sous-ensemble de Y.
- Déjà, on a toujours que f soit surjective ou non, f(f −1(B)) est inclus dans B. En effet :
- Soit y un élément de f(f −1(B))
- donc il existe un élément x de f −1(B) tel que f(x)=y
- comme x appartient à f −1(B) alors f(x) appartient à B
- d'où y appartient à B
- donc, f(f −1(B)) est inclus dans B
- Montrons maintenant que B est inclus dans f(f −1(B)) :
- soit y un élément de B
- f étant surjective, il existe un élément x de X tel que y=f(x)
- comme y appartient à B, f(x) appartient à B
- c'est-à-dire x appartient à f −1(B)
- d'où, f(x) appartient à f(f −1(B))
- i.e y appartient à f(f −1(B))
On a donc prouvé la double inclusion :
- f(f −1(B)) est inclus dans B
- B est inclus dans f(f −1(B))
Donc : f(f −1(B))= B
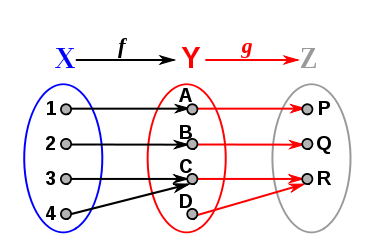
Surjectivité et composée
- Si
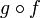 est surjective, alors g est surjective.
est surjective, alors g est surjective. - Si f et g sont surjectives, alors
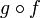 est surjective.
est surjective.
Les deux propriétés précédentes permettent de dire :
- que la surjectivité de g est une propriété nécessaire mais pas toujours suffisante pour que
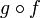 soit surjective,
soit surjective, - et que la surjectivité de f et de g est une condition suffisante mais pas toujours nécessaire pour que
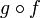 soit surjective.
soit surjective.
Soit f une application de X dans Y.
- f est surjective si et seulement si, pour toutes applications g et h de Y dans Z,
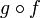 =
= 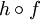 entraîne g = h.
entraîne g = h.
DémonstrationsSoient X, Y et Z trois ensembles et f : X→Y , g : Y→Z telles que
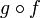 soit surjective.
soit surjective.Soit z un élément de Z, puisque
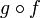 est surjective , il existe un élément x appartenant à X tel que : z=g[ f(x) ]
est surjective , il existe un élément x appartenant à X tel que : z=g[ f(x) ]En posant y = f(x), on a bien y est un élément de Y et z=g(y)
D'où, g est surjective.
Soient X, Y et Z trois ensembles et f:X→Y , g:Y→Z telles que f et g soient surjectives.
Soit z un élément de Z.
- g étant surjective, il existe un élément y appartenant à Y tel que : z=g(y)
- f étant surjective, il existe un élément x appartenant à X tel que : y=f(x)
Alors, z=g[ f(x) ]
Il existe donc un élément x de X tel que
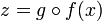
D'où,
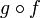 est surjective.
est surjective.La composée de deux surjections est encore une surjection.
Décomposition canonique
- Article détaillé : décomposition canonique dans l'article application
Toute application
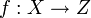 peut être décomposée comme
peut être décomposée comme 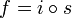 où s est une surjection et i une injection . Cette décomposition est unique à un isomorphisme près
où s est une surjection et i une injection . Cette décomposition est unique à un isomorphisme prèsCardinaux
Si f: X → Y est une fonction surjective, alors l'ensemble X a au moins autant d'éléments que l'ensemble Y, au sens des cardinaux. Cette affirmation nécessite d'admettre l'axiome du choix.
Voir aussi
- Portail des mathématiques
Catégorie : Théorie des ensembles
Wikimedia Foundation. 2010.


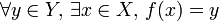
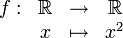
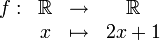
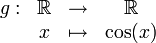
![\begin{matrix}h & \R & \rightarrow& [-1;1]\\ & x & \mapsto &\cos(x)\\\end{matrix}](/pictures/frwiki/97/a1c7e65b5fd50ab85f9929d577a43247.png)