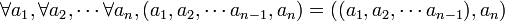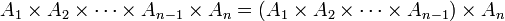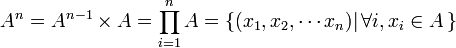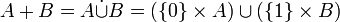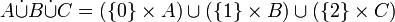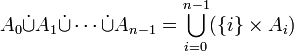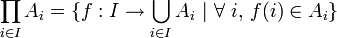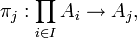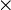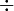- Ensemble-produit
-
Produit cartésien
- Cet article fait référence au concept mathématique sur les ensembles. Pour les graphes, voir produit cartésien de graphes.
En mathématiques, le produit cartésien de deux ensembles X et Y, appelé ensemble-produit, est l'ensemble de tous les couples, dont la première composante appartient à X et la seconde à Y. On généralise facilement la notion de produit cartésien binaire à celle de produit cartésien fini, qui est alors un ensemble de multiplets, on dit n-uplets pour les éléments d'un produit cartésien de n ensembles. On peut aussi introduire la notion de somme disjointe (ou cartésienne). Pour généraliser aux produits cartésiens infinis, des produits d'une famille quelconque (éventuellement infinie) d'ensembles, on a besoin de la notion de fonction.
Les produits cartésiens doivent leur nom à René Descartes, qui, en créant la géométrie analytique, a le premier utilisé ce que nous appelons maintenant,
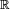 2 =
2 = 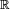 x
x 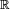 pour représenter le plan euclidien et
pour représenter le plan euclidien et 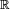 3 =
3 = 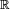 x
x 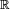 x
x 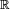 pour représenter l'espace euclidien tri-dimensionnel (
pour représenter l'espace euclidien tri-dimensionnel (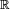 désigne la droite réelle).
désigne la droite réelle).Sommaire
Produit cartésien de deux ensembles
Définition
Pour tout ensemble A et tout ensemble B, il existe un unique ensemble dont les éléments sont les couples dont la première composante appartient à A et la seconde à B :
Cet ensemble est noté « A x B » (lire « A croix B ») et il est appelé produit cartésien de A par B.
Si on considère couples et produits cartésiens comme une notion primitive, on aura comme axiome cette propriété d'existence et d'unicité. Elle se démontre en théorie des ensembles, pour la représentation des couples choisie.
Exemple
Si A est l'ensemble { A, R, D, V, 10, 9, 8, 7, 6, 5, 4, 3, 2 } et B l'ensemble { pique, cœur, carreau, trèfle }, alors le produit cartésien de ces deux ensembles est un jeu classique de 52 cartes, soit l'ensemble suivant :
- { (A, pique) ... (2, pique) , (A, cœur) ... (2, coeur) , (A, carreau) ... (2, carreau) , (A, trèfle) ... (2, trèfle) }.
Propriétés
- On déduit directement de la définition que le produit cartésien d'un ensemble par l'ensemble vide est égal à l'ensemble vide, c'est à dire que pour tout ensemble A :
- Si A et B sont de cardinaux finis, alors le cardinal de A x B est égal au produit des cardinaux de A et de B.
- En règle générale, B x A ≠ A x B. Plus précisément, pour deux ensembles quelconques A et B :
- A x A est noté A2 (lire « A au carré ») et appelé carré cartésien de A :
A2 ne doit pas être confondu avec ΔA (lire « delta A »), diagonale de A :
Remarque : La diagonale d'un ensemble se confond avec son carré cartésien si et seulement si cet ensemble est vide ou se réduit à un singleton.
- Les sous-ensembles d'un produit cartésien sont appelés graphes.
Représentation en théorie des ensembles
En théorie des ensembles, si on choisit, comme usuellement, la représentation des couples de Kuratowski, les couples dont la première composante est dans A et la seconde dans B sont des éléments de
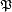 [
[ 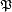 ( A
( A 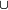 B ) ] (où
B ) ] (où 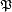 ( E ) désigne l' ensemble des parties de E). L'existence de cet ensemble résulte de l'axiome de la réunion et de l'axiome de l'ensemble des parties.
( E ) désigne l' ensemble des parties de E). L'existence de cet ensemble résulte de l'axiome de la réunion et de l'axiome de l'ensemble des parties.On peut donc définir le produit cartésien par compréhension, on aura bien sûr besoin des couples, donc, en plus des axiomes précédents, de l'axiome de la paire et du schéma d'axiomes de compréhension :
On peut aussi définir le produit cartésien en utilisant le schéma d'axiomes de remplacement au lieu de l'ensemble des parties[1] :
Représentation en théorie des catégories
Étant donnés deux objets S et T il y a au moins un objet P et deux fonctions p1 : P→S et p2 : P→T tels que pour tout objet X et toutes fonctions f1 : X→S et f2 : X→T existe une unique fonction f: X→P telle que f1 = p1 o f et f2 = p2 o f ; P n'est pas défini de façon unique cependant toutes les structures ainsi obtenues sont isomorphes, ce qui permet de définir le produit cartésien SxT ; un couple est alors un élément de SxT ; si p1(M) = s et p2(M) = t on note M=(s,t)[2],[3].
Généralisation à plus de deux ensembles
Triplets
Comme pour les couples, l'important, c'est leur propriété fondamentale : deux triplets sont égaux si et seulement si leurs premières composantes sont égales entre elles, puis leurs deuxièmes composantes, et enfin leurs troisièmes :
Là encore, cette propriété ne suffit pas à définir la notion de triplet, et là encore, plusieurs définitions incompatibles entre elles sont possibles a priori. On pose habituellement :
Produit cartésien de trois ensembles
Il est défini par :
D'après ce qui précède, A x B x C = ( A x B ) x C. Là encore l'ordre des termes est important. Le produit A x A x A est appelé cube cartésien de A et il est noté A3 (lire « A au cube ») :
Multiplets
Les définitions précédentes se généralisent par récurrence :
- Propriété fondamentale d'un multiplet d'ordre n, ou n-uplet :
- Définition d'un n-uplet :
- Produit cartésien de n ensembles :
- Puissance cartésienne n-ième d'un ensemble :
Note : en peut définir des produits cartésiens infinis (voir ci-dessous), mais pour le faire, nous avons besoin de la notion de fonction.
Somme disjointe
Dans une réunion d'ensembles A∪B, l'origine des éléments y figurant est perdue. Un moyen d'éviter cette perte d'information est de réunir non pas directement les ensembles de départ, mais des copies de ces ensembles de la forme { α } × A et { β } × B , où « α » et « β » sont deux symboles quelconques distincts servant à identifier les ensembles A et B, par exemple « Ø » et « { Ø } », ou « 0 » et « 1 ».
L'union disjointe, encore appelée somme disjointe ou somme cartésienne de deux ensembles A et B est ainsi définie par :
On peut remarquer que la somme disjointe de deux ensembles vérifie également la propriété fondamentale des couples. De plus, contrairement aux couples de Kuratowski, cette notion, qui n'utilise que des opérations ensemblistes élémentaires, peut s'appliquer aux classes propres. C'est pourquoi les sommes disjointes sont parfois appelées couples généralisés, et utilisées ainsi en théorie des classes.
La somme disjointe peut se généraliser à plus de deux ensembles. Par exemple, pour trois ensembles quelconques A, B et C:
On rappelle que l'entier de von Neumann 2 peut se définir comme {Ø, {Ø}} . Plus généralement, l'entier de von Neumann n étant défini, l'entier de von Neumann n+1 est défini par n+1 = n ∪ {n}.
On peut donc généraliser ce qui précède et définir ainsi la somme disjointe de n ensembles
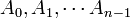 quelconques :
quelconques :D'autre part cette définition de la somme disjointe utilise les entiers de la théorie des ensembles, non ceux du méta-langage. On peut donc également généraliser cette notion à des ensembles quelconques (non nécessairement finis) d'indices, par exemple des réunions disjointes dénombrables.
La définition de la somme disjointe souffre d'un arbitraire inessentiel. On peut définir la somme disjointe comme étant la réunion
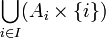 ou bien
ou bien 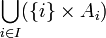 . Ces deux possibilités correspondent respectivement à un marquage « à droite » ou « à gauche » des éléments de la réunion
. Ces deux possibilités correspondent respectivement à un marquage « à droite » ou « à gauche » des éléments de la réunion 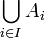 selon l'indice associé à l'ensemble dont ils proviennent. Dans les deux cas, la somme disjointe peut être mise en bijection avec la réunion. (Voir la section famille d'ensembles pour la notation)
selon l'indice associé à l'ensemble dont ils proviennent. Dans les deux cas, la somme disjointe peut être mise en bijection avec la réunion. (Voir la section famille d'ensembles pour la notation)Produits infinis
On peut généraliser la notion de produit cartésien à celle de produit d'une famille d'ensembles indexée par un ensemble quelconque, fini ou infini.
Bien que plus générale, cette notion peut difficilement être introduite en théorie des ensembles avant celle de produit cartésien binaire, du moins naturellement, car elle fait appel à la notion de fonction, qui utilise à son tour justement celle de couple, et donc de produit cartésien binaire.[4]
Famille d'ensembles
Une famille A d'ensembles indexée par un ensemble I est une fonction définie sur I. L'image de i par A est notée Ai. Il s'agit juste d'une notation (adaptée à un certain usage) pour une construction connue.
- La famille A indexée par I sera plutôt notée { Ai }
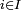 . Au sens de la théorie des ensembles, la famille { Ai }
. Au sens de la théorie des ensembles, la famille { Ai }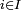 peut être assimilée à son graphe, l'ensemble des couples ( i, Ai ), pour
peut être assimilée à son graphe, l'ensemble des couples ( i, Ai ), pour 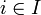 .
.
- Toutefois, la réunion d'une famille { Ai }
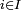 , notée
, notée 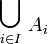 , désigne bien la réunion des images Ai de la famille en tant que fonction, et non celle des éléments de la famille en tant que graphe, qui sont au sens strict les couples ( i, Ai ).
, désigne bien la réunion des images Ai de la famille en tant que fonction, et non celle des éléments de la famille en tant que graphe, qui sont au sens strict les couples ( i, Ai ).
Produit cartésien d'une famille d'ensembles
On peut maintenant définir le produit cartésien d'une famille d'ensembles { Ai } i∈I, que l'on note habituellement
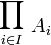 , ou parfois
, ou parfois 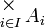 .
.Il s'agit de l'ensemble des fonctions f de I dans la réunion de la famille, telles que pour tout i dans I, f(i) appartienne à Ai :
- Pour utiliser cette définition, il faut pouvoir extraire d'un élément du produit sa composante d'index j, élément de I.
Pour cela, on définit pour tout j dans I, la fonction appelée j-ème projection,
par :
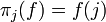 .
.
- On peut énoncer l'axiome du choix ainsi : le produit d'une famille d'ensembles non vides est non vide.
Notes et références
- ↑ Harvey Friedman.
- ↑ Baez, quantum, node 4
- ↑ Colin McLarty, Elementary Categories, Elementary Toposes, Clarendon Press, Oxford, 1995.
- ↑ Une fonction de A dans B est souvent introduite comme un triplet ( A, B, C ), où C est un sous-ensemble du produit cartésien A × B, appelé graphe de la fonction et tel que tout élément de A figure (en première composante) dans exactement un couple de C. En pratique toutefois, s'il n'y a pas de risque d'ambiguïté, on peut par abus de langage assimiler la fonction à son graphe C. D'ailleurs en théorie des ensembles on définit souvent une fonction directement comme un ensemble de couples. La pratique est cohérente — être une fonction de A dans B devient alors une propriété de la fonction — mais pas à conseiller dans les cours d'introduction aux mathématiques.
Voir aussi
- Mathématiques -- Théorie des ensembles
- Notion d'ensemble
- Sous-ensembles
- Opérations sur les ensembles
- Couple
- Correspondance et relation
- Portail des mathématiques
Catégories : Théorie des ensembles | Opération
Wikimedia Foundation. 2010.

![\forall A \; \forall B \; \exists! P\;\forall x \; \forall y \;[( x \in A \wedge y \in B ) \Leftrightarrow ( x , y ) \in P]](/pictures/frwiki/97/a7483b1789c4bfb820be5395c01c7d72.png)
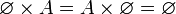
![[A \times B \ne B \times A] \Leftrightarrow [( A \ne B ) \wedge ( A \ne \varnothing ) \wedge ( B \ne \varnothing )]](/pictures/frwiki/51/3815207e3f1188c8852ff19104122441.png)
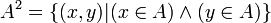
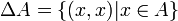
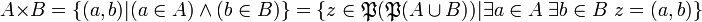
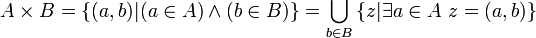
![\forall a , \forall b , \forall c , \forall d , \forall e , \forall f , [\, ( a , b , c ) = ( d , e , f ) \,] \Leftrightarrow [\, ( a = d ) \wedge ( b = e ) \wedge ( c = f ) \,]](/pictures/frwiki/98/bef8730ac4c582baa5dd2c30cda5405f.png)
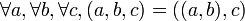
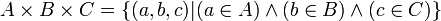
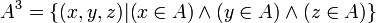
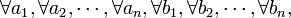
![[\, ( a_{1} , a_{2} , \cdots a_{n} ) = ( b_{1} , b_{2} , \cdots b_{n} ) \,] \Leftrightarrow [\, ( a_{1} = b_{1} ) \wedge ( a_{2} = b_{2} ) \wedge \cdots ( a_{n} = b_{n} ) \,]](/pictures/frwiki/97/a56e56b787f7015fdcc47f29fb517597.png)