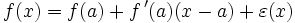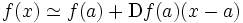Développement limité d'ordre 1

Développement limité d'ordre 1

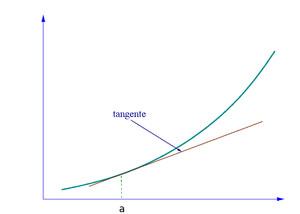
Approximation linéaire

Tangente au point (a, f(a))

En mathématiques, une approximation linéaire est une approximation d'une fonction, par une fonction affine.

Par exemple, étant donné une fonction dérivable f d'une variable réelle, et un réel a, il existe une fonction \varepsilon définie dans un voisinage de a telle que

f(x)=f(a)+f\,'(a)(x - a)+\varepsilon(x)

\varepsilon s'appelle le reste. Cette formule apparaît comme un cas particulier (n = 1) de la formule de Taylor : c'est un développement limité d'ordre 1.

Une approximation linéaire de f s'obtient en négligeant le reste. La fonction 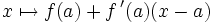x\mapsto f(a) + f\,'(a)(x-a) représente alors une approximation linéaire de f en a.

On écrit alors, pour x dans un voisinage de a

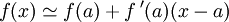f(x) \simeq f(a)+f\,'(a)(x-a).

L'expression de droite correspond à l'équation 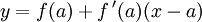y=f(a)+f\,'(a)(x-a) de la tangente à la courbe représentative de f au point (a,f(a)), et pour cette raison, certains appellent cette méthode l'approximation tangente ou approximation affine tangente.

Il est aussi possible d'utiliser des approximations pour les fonctions vectorielles d'une variable vectorielle, dans laquelle 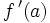f\,'(a) est remplacée par une matrice jacobienne. L'approximation correspond alors à l'équation d'une droite tangente, ou d'un plan tangent, ou d'un hyperplan tangent. Cela s'applique aussi aux fonctions d'une variable complexe.

Dans le cas plus général des espaces de Banach, on peut écrire

f(x) \simeq f(a) + \mathrm Df(a)(x - a)

où Df(a) est la différentielle de f en a. Ici l'application linéaire n'est autre que Df(a).

Exemples

Pour trouver une valeur approchée de \sqrt[3]{25} il est possible de procéder de la manière suivante:

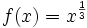  1. considérer la fonction f définie par f(x)= x^{1\over 3}\,. Le problème se ramène à la recherche d'une valeur approchée de f(25).
  2. f est une fonction puissance donc dérivable sur 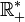\R_+^* et la dérivée est donnée par
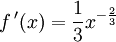    f\,'(x)= \frac13 x^{-\frac23}.
  3. Par l'approximation linéaire donnée par la dérivée, il vient, en prenant a = 27 :
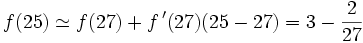    f(25) \simeq f(27) + f\,'(27)(25 - 27) = 3 - \frac2{27}.
  4. La valeur approchée 2,926 obtenue, apparaît assez proche de la valeur exacte 2,924…
Ce document provient de « Approximation lin%C3%A9aire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Développement limité d'ordre 1 de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Developpement limite — Développement limité En physique et en mathématiques, un développement limité (noté D.L.) d une fonction f au voisinage d un point, est une approximation polynomiale de cette fonction en ce point, c est à dire l écriture de cette fonction sous la …   Wikipédia en Français

  • Développement Limité — En physique et en mathématiques, un développement limité (noté D.L.) d une fonction f au voisinage d un point, est une approximation polynomiale de cette fonction en ce point, c est à dire l écriture de cette fonction sous la forme de la… …   Wikipédia en Français

  • Développement limité — En physique et en mathématiques, un développement limité (noté DL) d une fonction f au voisinage d un point, est une approximation polynomiale de cette fonction en ce point, c est à dire l écriture de cette fonction sous la forme de la… …   Wikipédia en Français

  • Développement illimité — Développement limité En physique et en mathématiques, un développement limité (noté D.L.) d une fonction f au voisinage d un point, est une approximation polynomiale de cette fonction en ce point, c est à dire l écriture de cette fonction sous la …   Wikipédia en Français

  • développement — [ dev(ə)lɔpmɑ̃ ] n. m. • XVe, répandu XVIIe XVIIIe; de développer A ♦ (Spatial) 1 ♦ Rare Action de donner toute son étendue à (qqch.). ⇒ déployer, dérouler. Le développement d une pièce d étoffe. (1694) …   Encyclopédie Universelle

  • Ordre de Citeaux — Ordre cistercien Pour les articles homonymes, voir SOC. Armes de l ordre de Cîteaux L’ordre cistercien (Ordo cisterciensis, o.cist.), également connu s …   Wikipédia en Français

  • Ordre de Cîteaux — Ordre cistercien Pour les articles homonymes, voir SOC. Armes de l ordre de Cîteaux L’ordre cistercien (Ordo cisterciensis, o.cist.), également connu s …   Wikipédia en Français

  • Ordre cistercien — Pour les articles homonymes, voir SOC. Armes de l ordre de Cîteaux L’ordre cistercien (Ordo cisterciensis, o.cist.), également connu sous le nom d’ordre de Cîteaux ou encore de saint ordre …   Wikipédia en Français

  • Développement asymptotique — En mathématiques, un développement asymptotique d une fonction f donnée dans un voisinage fixé est une somme finie de fonctions de références qui donne une bonne approximation du comportement de la fonction f dans le voisinage considéré. Le… …   Wikipédia en Français

  • Développement de Laplace — Comatrice En algèbre linéaire, la comatrice d une matrice carrée A est une matrice introduite par une généralisation du calcul de l inverse de A. Elle a une importance considérable pour l étude des déterminants. Ses coefficients sont appelés… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”