- Degre d'une application
-
Degré d'une application
 Pour les articles homonymes, voir degré.
Pour les articles homonymes, voir degré.Le degré d'une application continue entre variétés de même dimension est une généralisation de la notion d'enroulement d'un cercle sur lui-même. C'est un invariant homologique à valeurs entières positives.
Sa définition, d'abord réservée aux applications différentiables, s'étend aux applications continues par passage à la limite du fait de son invariance par homotopie. Mais la construction des groupes d'homologie permet aussi de proposer une définition directe pour les applications continues.
Sommaire
Enroulement
Il existe plusieurs manières de considérer le cercle comme un quotient de la droite réelle :
- l'ensemble des classes d'équivalences modulo 1 (deux nombres réels étant équivalents si leur différence est un entier relatif) forme le cercle noté
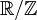 ;
; - le cercle unité
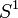 du plan
du plan 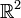 est l'image de
est l'image de  par l'application
par l'application 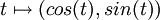 , interprétation réelle de l'exponentielle complexe.
, interprétation réelle de l'exponentielle complexe.
Cette description est équivalente au quotient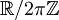 .
.
Pour toute application continue
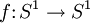 , il existe une application continue
, il existe une application continue 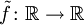 , appelée relèvement de f dans
, appelée relèvement de f dans  , telle que pour tout réel x,
, telle que pour tout réel x, ![f([x]) = [\tilde{f}(x)]](/pictures/frwiki/97/a1f6844612ea7543d91986ef08030b5a.png) . Ce relèvement est unique à une constante additive près (multiple de 2π).
. Ce relèvement est unique à une constante additive près (multiple de 2π).Puisque la fonction
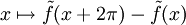 est continue et que ses valeurs sont des multiples entiers de 2π, elle est constante et la valeur de ce multiple est appelée degré d'enroulement de la fonction f.
est continue et que ses valeurs sont des multiples entiers de 2π, elle est constante et la valeur de ce multiple est appelée degré d'enroulement de la fonction f.En géométrie différentielle
Définition
Soient M et N deux variétés différentielles (sans bord) orientées et de même dimension, telles que M soit compacte et N soit connexe.
Soit f une application différentiable de M dans N.
(La définition peut aussi s'étendre aux variétés à bord à condition que la fonction f préserve le bord.)D'après le théorème de Sard, il existe un point y de N qui soit une valeur régulière de f.
En tout point x de la préimage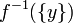 , la différentielle
, la différentielle 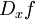 induit donc une application linéaire surjective entre les espaces tangents (orientés)
induit donc une application linéaire surjective entre les espaces tangents (orientés) 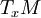 et
et 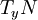 .
.
Par égalité des dimensions, ces applications linéaires sont des isomorphismes d'espaces vectoriels orientés.
Leur signe, noté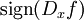 , est défini par
, est défini par 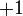 si
si 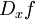 préserve l'orientation et
préserve l'orientation et 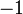 dans le cas contraire.
dans le cas contraire.
Par compacité de M, la préimage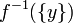 est finie et le degré de f en y peut donc se définir par la somme :
est finie et le degré de f en y peut donc se définir par la somme :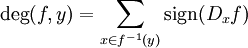 .
.
Si les variétés M ou N ne sont pas orientées, le degré de f en une valeur régulière y peut simplement se définir par la parité du cardinal de la préimage, autrement dit :
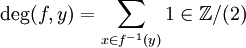 .
.
Le résultat de ce calcul est indépendant du choix de la valeur régulière. Le degré de f est donc noté simplement
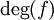 .
.Exemples
- L'application identité est de degré 1.
- L'application antipodale sur la sphère Sn est de degré ( − 1)n + 1.
- Si l'application f n'est pas surjective, un point de N qui n'est pas dans l'image de f est une valeur régulière donc le degré de f vaut zéro.
C'est notamment le cas si N est non-compacte, ou si f est constante et N non réduite à un point. - Si f est un revêtement de variétés différentielles compactes orientables sans bord, le degré de f est égal au nombre de feuillets.
Invariance par homotopie
L'intérêt principal de cette notion réside dans le fait que si deux applications sont homotopes, elles ont même degré.
Par conséquent, les sphères Sn ne sont pas contractiles et l'application antipodale n'est pas homotope à l'identité sur les sphères paires.
Le degré constitue même un invariant complet pour les sphères : deux applications de Sn dans Sn sont homotopes si et seulement si elles ont même degré.
Article détaillé : Groupes d'homotopie des sphères.En topologie algébrique
Définition
Soit M et N deux variétés compactes orientées et de même dimension n, dont les classes d'orientation respectives sont notées [M] et [N]. La condition d'orientation peut être retirée si les groupes d'homologie sont calculés à coefficients dans
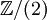 .
.
Si la variété N est connexe, la classe [N] est un générateur du groupe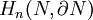 .
.
Soit f une application continue de M dans N qui préserve le bord. L'application f * induite en homologie associe à la classe [M] un élément λ[N] de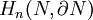 .
.Le nombre λ est alors appelé degré de f et noté
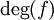 .
.La propriété d'excision de l'homologie permet de montrer que cette définition étend celle donnée par la géométrie différentielle.
Plus généralement, la notion de degré peut être étendue à toute application entre paires d'espaces munis de classe génératrice d'un groupe d'homologie en une dimension fixée. Ceci permet notamment de parler de degré pour une application entre complexes de Poincaré ou entre espaces de Thom.
Propriétés
Le degré est donc un invariant homologique.
Par dualité de Poincaré en utilisant la cohomologie de De Rham, le degré peut aussi s'obtenir en intégrant sur la variété source une forme volume de la variété but.
- Portail des mathématiques
Catégories : Géométrie différentielle | Invariant | Homologie - l'ensemble des classes d'équivalences modulo 1 (deux nombres réels étant équivalents si leur différence est un entier relatif) forme le cercle noté
Wikimedia Foundation. 2010.
