Préimage
- Préimage
-
Antécédent (mathématiques)
Définition
En mathématiques, étant donnés deux ensembles non vides E, F et une application 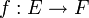 , on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que
, on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que 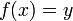 .
.
Un antécédent est donc, par définition, un élément de l'image réciproque 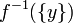 .
.
Exemples
- Soient la fonction
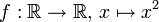 et y un réel.
et y un réel.
- Si y > 0, y admet deux antécédents, qui sont
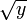 et
et 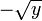
- Si y = 0, y admet un seul antécédent, qui est 0
- Si y < 0, y n'admet aucun antécédent
- Soient E un ensemble non vide, et une application
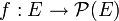 , où
, où 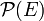 désigne l'ensemble des parties de E. On définit
désigne l'ensemble des parties de E. On définit 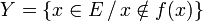 : Y est une partie de E, autrement dit un élément de l'ensemble
: Y est une partie de E, autrement dit un élément de l'ensemble 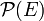 .
.
- Cet élément n'admet aucun antécédent par f. En effet, supposons qu'un tel antécédent
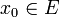 existe. On a donc
existe. On a donc 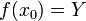 .
.
- Deux cas sont possibles :
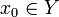 , ce qui veut dire (par définition de Y) que
, ce qui veut dire (par définition de Y) que 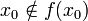 , ou
, ou 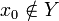
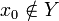 , ce qui veut dire (par définition de Y) que
, ce qui veut dire (par définition de Y) que 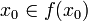 , ou
, ou 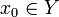
- Dans les deux cas, on aboutit à une contradiction, ce qui prouve par l'absurde que Y n'a pas d'antécédent (cf. l'argument de la diagonale de Cantor).
Image d'un ensemble par une application
Soient une application 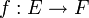 et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note
et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note 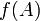 :
:
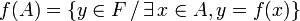 .
.
En particulier, l'image de E par f, appelée image de f, est l'ensemble des éléments y de F qui admettent au moins un antécédent :
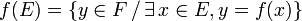 .
.
Injections, surjections, bijections
Soit une application 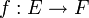 .
.
- On dit que f est injective, ou que c'est une injection, si tout élément de F admet au plus un antécédent.
- On dit que f est surjective, ou que c'est une surjection, si tout élément de F admet au moins un antécédent, c'est-à-dire si
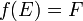 .
.
- On dit que f est bijective, ou que c'est une bijection, si tout élément de F admet un antécédent et un seul, c'est-à-dire si f est à la fois injective et surjective.
- Dans ce cas, on peut définir l'application
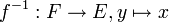 , où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.
, où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.
(l'exemple vu plus haut montre qu'il n'existe aucune application surjective 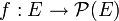 ).
).
Voir aussi
Catégorie : Théorie des ensembles
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Préimage de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
preimage — noun The set containing exactly every member of the domain of a function such that the member is mapped by the function onto an element of a given subset of the codomain of the function. Formally, of a subset B of the codomain Y under a function… … Wiktionary
Preimage attack — In cryptography, a preimage attack on a cryptographic hash is an attempt to find a message that has a specific hash value. There are two types of preimage attacks:* First preimage attack : given a hash h , find a message m such that hash(m) = h … Wikipedia
Preimage-Angriff — Urbild Angriffe (auch engl. preimage attack) sind Angriffe auf eine kryptologische Hashfunktion mit dem Ziel, zu einem gegebenen Hash einer unbekannten Nachricht (Erstes Urbild Angriff, auch engl. first preimage attack) oder zu einer gegebenen… … Deutsch Wikipedia
Preimage theorem — In mathematics, particularly in differential topology, the preimage theorem is a theorem concerning the preimage of particular points in a manifold under the action of a smooth map.tatement of Theorem Definition. Let f: X o Y,! be a smooth map… … Wikipedia
preimage — n. * * * … Universalium
preimage — n … Useful english dictionary
One-way compression function — In cryptography, a one way compression function is a function that transforms two fixed length inputs to an output of the same size as one of the inputs. The transformation is one way , meaning that it is difficult given a particular output to… … Wikipedia
Function (mathematics) — f(x) redirects here. For the band, see f(x) (band). Graph of example function, In mathematics, a function associates one quantity, the a … Wikipedia
Implementation of mathematics in set theory — This article examines the implementation of mathematical concepts in set theory. The implementation of a number of basic mathematical concepts is carried out in parallel in ZFC (the dominant set theory) and in NFU, the version of Quine s New… … Wikipedia
Image (mathematics) — In mathematics, the image of a preimage under a given function is the set of all possible function outputs when taking each element of the preimage, successively, as the function s argument. DefinitionIf f : X → Y is a function from set X to set… … Wikipedia
 Pour les articles homonymes, voir Antécédent.
Pour les articles homonymes, voir Antécédent.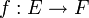 , on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que
, on appelle antécédent (par f) d'un élément y de F tout élément x de E tel que 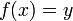 .
.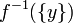 .
.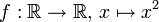 et y un réel.
et y un réel.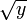 et
et 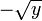
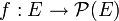 , où
, où 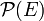 désigne l'ensemble des parties de E. On définit
désigne l'ensemble des parties de E. On définit 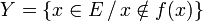 : Y est une partie de E, autrement dit un élément de l'ensemble
: Y est une partie de E, autrement dit un élément de l'ensemble 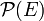 .
.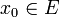 existe. On a donc
existe. On a donc 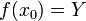 .
.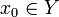 , ce qui veut dire (par définition de Y) que
, ce qui veut dire (par définition de Y) que 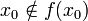 , ou
, ou 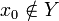
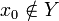 , ce qui veut dire (par définition de Y) que
, ce qui veut dire (par définition de Y) que 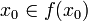 , ou
, ou 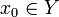
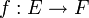 et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note
et A un sous-ensemble de E. On appelle image de A par f l'ensemble des éléments y de F qui admettent au moins un antécédent appartenant à A ; on la note 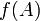 :
: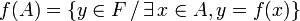 .
.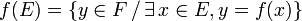 .
.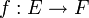 .
.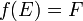 .
.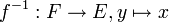 , où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.
, où x est l'unique antécédent de y par f. C'est aussi une bijection, dite réciproque de f.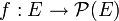 ).
).