Courbe de Bézier

Exemple de construction de courbe de Bézier

Les courbes de Bézier sont des courbes polynomiales paramétriques décrites pour la première fois en 1962 par l'ingénieur français Pierre Bézier qui les utilisa pour concevoir des pièces d'automobiles à l'aide d'ordinateurs. Elles ont de nombreuses applications dans la synthèse d'images et le rendu de fontes. Elles ont donné naissance à de nombreux autres objets mathématiques.

Il existait avant Bézier des courbes d'ajustement nommées splines, mais dont le défaut était de changer d'aspect lors d'une rotation de repère, ce qui les rendait inutilisables en CAO. Bézier partit d'une approche géométrique fondée sur la linéarité de l'espace euclidien et la théorie, déjà existante, du barycentre : si la définition est purement géométrique, aucun repère n'intervient puisque la construction en est indépendante, ce qui n'était pas le cas pour les splines (les splines conformes aux principes de Bézier seront par la suite nommées B-splines).

Sommaire

1 Théorie générale
2 Technique
3 Exemples
4 Applications
5 Courbe de Bézier rationnelle
6 Notes
7 Voir aussi
- 7.1 Articles connexes
- 7.2 Liens externes
8 Références

Théorie générale

Pour n+1 points de contrôle ( $\mathbf{P}_0, \dots, \mathbf{P}_n$ ), on définit une courbe de Bézier par l'ensemble des points $\sum_{i = 0}^n B_i^n(t) . \mathbf{P}_i$ , avec $t \in[0, 1]$ et où les $B_i^n$ sont les polynômes de Bernstein.

La suite des points $\mathbf{P}_0, \dots, \mathbf{P}_n$ forme le « polygone de contrôle de Bézier ».

Remarque: Puisque $\sum_{i=0}^n B_i^n(t) = 1$ , alors la courbe est correctement définie.; Chaque point de la courbe peut être vu alors comme un barycentre (une moyenne pondérée) des m+1 points de contrôle, ceux-ci étant alors pondérés d'un poids égal à l’image par le polynôme de Bernstein associé à chaque point de contrôle de la même valeur du paramètre t caractérisant un point de la courbe, la somme de ces m+1 poids valant alors exactement 1.

Propriétés^[1] :

La courbe est à l'intérieur de l'enveloppe convexe des points de contrôle.
La courbe commence par le point $\mathbf{P}_0$ et se termine par le point $\mathbf{P}_n$ , mais ne passe pas a priori par les autres points de contrôle qui déterminent cependant l'allure générale de la courbe.
$\overrightarrow{P_0P_1}$ est le vecteur tangent à la courbe en $\mathbf{P}_0$ et $\overrightarrow{P_{n-1}P_n}$ au point $\mathbf{P}_n$ .
Une courbe de Bézier est infiniment dérivable (de classe $C^{\infty}$ ).
La courbe de Bézier est un segment si et seulement si les points de contrôle sont alignés.
Chaque restriction d'une courbe de Bézier est aussi une courbe de Bézier.
Un arc de cercle (ni même aucun arc de courbe conique, en dehors du segment de droite) ne peut pas être décrit par une courbe de Bézier, quel que soit son degré.
Le contrôle de la courbe est global : modifier un point de contrôle modifie toute la courbe, et non pas un voisinage du point de contrôle.
Pour effectuer une transformation affine de la courbe, il suffit d'effectuer la transformation sur tous les points de contrôle.

Technique

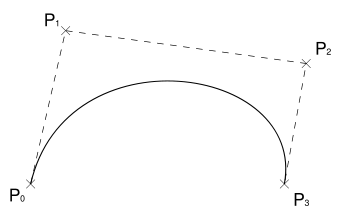
Quatre points P₀, P₁, P₂ et P₃ définissent une courbe de Bézier cubique. La courbe se trace en partant du point P₀, en se dirigeant vers P₁ et en arrivant au point P₃ selon la direction P₂-P₃. En général, la courbe ne passe ni par P₁ ni par P₂ : ces points sont simplement là pour donner une information de direction. La distance entre P₀ et P₁ détermine la « longueur » du déplacement dans la direction de P₁ avant de tourner vers P₃.

La forme paramétrique de la courbe s'écrit:

$\mathbf{P}(t)= \mathbf{P}_0(1-t)^3 + 3 \mathbf{P}_1 t(1-t)^2 + 3 \mathbf{P}_2 t^2(1-t) + \mathbf{P}_3 t^3$

pour 0 ≤ t ≤ 1. Remarquons que les coefficients binomiaux apparaissent dans l'ordre (1, 3, 3, 1). La formule est inspirée d'une loi binomiale et montre que la courbe est toujours complètement contenue dans l'enveloppe convexe des quatre points donnés. Les courbes de Bézier sont intéressantes pour le traitement des images pour deux raisons principales :

Les points peuvent être rapidement calculés en utilisant une procédure récursive qui utilise la division par deux et les opérations de base en évitant toutes les opérations de l'arithmétique des nombres réels flottants.

$\begin{pmatrix}A'\\B'\\C'\\D'\end{pmatrix}=\begin{pmatrix}1&0&0&0\\{1\over 2}&{1\over 2}&0&0\\{1\over 4}&{2\over 4}&{1\over 4}&0\\{1\over 8}&{3\over 8}&{3\over 8}&{1\over 8}\end{pmatrix}\cdot\begin{pmatrix}A\\B\\C\\D\end{pmatrix}$

                       ,
           ,

Plus précisément, on peut décomposer la courbe P(t) en deux courbes P_L et P_R dont les points de contrôles sont respectivement (L₁, L₂,L₃,L₄) et (R₁, R₂,R₃,R₄) avec

$\begin{pmatrix}L_1'\\L_2'\\L_3'\\L_4'\end{pmatrix}=\begin{pmatrix}1&0&0&0\\{1\over 2}&{1\over 2}&0&0\\{1\over 4}&{2\over 4}&{1\over 4}&0\\{1\over 8}&{3\over 8}&{3\over 8}&{1\over 8}\end{pmatrix}\cdot\begin{pmatrix}A\\B\\C\\D\end{pmatrix}$ et $\begin{pmatrix}R_1'\\R_2'\\R_3'\\R_4'\end{pmatrix}=\begin{pmatrix} {1\over 8}&{3\over 8}&{3\over 8}&{1\over 8}\\ 0&{1\over 4}&{2\over 4}&{1\over 4}\\ 0&0&{1\over 2}&{1\over 2}\\ 0&0&0&1 \end{pmatrix}\cdot\begin{pmatrix}A\\B\\C\\D\end{pmatrix}$

Bezier rec.png

Lors de cet appel récursif pour tracer P(t), étant donné que la courbe de Bézier passe par le premier et le dernier point de contrôle, la position des extrémités de chaque morceau (L₁, L₄=R₁ et R₄) est connue. Lorsque l'on implémente un tel tracé, le critère d'arrêt de la récurrence peut être lié à la distance entre la sous-courbe à tracer et le segment [L₁,L₄] par exemple.

Note: l'arithmétique des nombres réels flottants étant disponible directement sur les processeurs modernes, elle est devenue bien plus rapide que l'allocation de mémoire nécessaire pour une récursion. De plus, une méthode qui fournit les pixels de la courbe à tracer sans aller de proche en proche ne permet pas d'antialiasing. La récursion n'est donc plus la bonne méthode pour tracer les courbes de Bézier ; on utilisera avantageusement la méthode qui parcourt les pixels de proche en proche en calculant à chaque pas un "défaut de tangente" utilisable pour l'antialiasing.

Le calcul d'un point d'une courbe de Bézier peut également s'effectuer en utilisant la méthode de Horner en calculant préalablement les coefficients vectoriels $\mathbf{a_i}$ du polynôme:

$\mathbf{a_i}=\begin{pmatrix}m\\i\end{pmatrix}\sum_{j=0}^{i} (-1)^{i-j} \begin{pmatrix}i\\j\end{pmatrix} \mathbf{P_j} \qquad \mbox{pour} \qquad i=0...m$

Un exemple de programme en TI-Basic pour tracer des courbes de Bézier sur TI (82 a 84+)

ClrHome

ClrList L1

ClrList L2

Input "NB DE POINT N=?",N

N→dim L1

N→dim L2

N-1→N

For(K,0,N

ClrHome

Disp "POINT PI (XI,YI)

Output(1,8,K

Output(1,12,K

Output(1,15,K

Prompt X

X→L1(K+1

Prompt Y

Y→L2(K+1

End

min(L1→Xmin

max(L1→Xmax

(Xmax-Xmin)/8→Xscl

min(L2→Ymin

max(L2→Ymax

(Ymax-Ymin)/8→Yscl

"sum (seq(((N nCr I)*T^I*(1-T)^(N-I))*L1(I+1),I,0,N,1))"→X1T

"sum (seq(((N nCr I)*T^I*(1-T)^(N-I))*L2(I+1),I,0,N,1))"→Y1T

0→Tmin

1→Tmax

(25N)^-1→Tstep

Param

Connected

FullScreen

For(K,1,N

Line(L1(K),L2(K),L1(K+1),L2(K+1

End

Line(L1(N+1),L2(N+1),L1(1),L2(1

DispGraph

Les → correspondent à la touche "sto→" qui se trouve juste au dessus de la touche "On". Chaque point P_i est enregistré par ses deux coordonnées (x_i,y_i) dans les deux listes L1 et L2, et la courbe de Bézier sera tracée en paramétrique à l'aide de la formule donnée plus haut. Les "Line" finaux permettent de dessiner l'enveloppe convexe dans laquelle se trouve la courbe.

Exemples

Courbe de Bézier linéaire (de degré 1)

Les points de contrôle P₀ et P₁ définissent la courbe de Bézier donnée par l'équation :

$\mathbf{B}(t)=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1].$

Il s'agit donc du segment [P0, P1].

Courbe de Bézier quadratique (de degré 2)

Une courbe de Bézier quadratique est la courbe B(t) définie par les points de contrôle P₀, P₁ et P₂.

$\mathbf{B}(t) = (1 - t)^{2}\mathbf{P_0} + 2t(1 - t)\mathbf{P_1} + t^{2}\mathbf{P_2} \mbox{ , } t \in [0,1].$

Ces courbes quadratiques sont encore très utilisées aujourd'hui (par exemple dans les définitions de glyphes des polices de caractères au format TrueType, et les polices OpenType dans leur variété compatible TrueType).

Toutefois, si elles permettent d'assurer la continuité en tangence de deux courbes raccordées, elles ne permettent pas (en général) de conserver la continuité de la courbure aux points d'interconnexion. Pour pallier cet inconvénient, il est alors nécessaire d'augmenter le nombre d'arcs interconnectés afin de réduire les ruptures de courbure entre chacun d'eux, ce qui en limite l'intérêt et peut conduire à une complexification de la conception des courbes (avec davantage de sommets et de points de contrôles à positionner).

Courbe de Bézier cubique (de degré 3)

Une courbe de Bézier cubique est la courbe B(t) définie par les points de contrôle P₀, P₁, P₂ et P₃. Sa forme paramétrique est :

$\mathbf{B}(t)=\mathbf{P_0}(1-t)^3+3\mathbf{P_1}t(1-t)^2+3\mathbf{P_2}t^2(1-t)+\mathbf{P_3}t^3 \mbox{ , } t \in [0,1].$

Ce sont les courbes de Bézier les plus utilisées en conception graphique (car elles permettent d'assurer non seulement la continuité en tangence de deux courbes raccordées, mais aussi celle de leur courbure, tout en évitant d'avoir à positionner de nombreux sommets et points de contrôle).

Elles sont utilisées par exemple dans le langage PostScript et la définition des glyphes des polices de caractères de « type 1 », ainsi que dans les polices OpenType dans leur variété CFF (Compact Font Format) qui reprend les mêmes définitions de sommets et points de contrôle.

Courbe de Bézier de degré supérieur à 3: Elles sont rarement utilisées. On préfère se ramener à l'utilisation de courbes cubiques que l'on raccorde afin de conserver le bénéfice de la continuité de courbure. Pour cela, il faut et il suffit que le dernier point d'une courbe soit le premier d'une autre. On obtient ainsi une courbe continue.; Par exemple, pour une courbe définie par les points A, B, C, D, E, F et G, on utilise les courbes cubiques définies par A, B, C, et D, et par D, E, F, et G et la continuité est ainsi assurée. Pour avoir une courbe C¹ en D, il faut que [C, D] = [D, E], et si en plus on veut qu'elle soit C² en D, alors [B, D] = [D, F], et de même pour les dérivées successives. Toutefois, cette transformation fait perdre la continuité C³ en D (et la seule façon d'y pallier est d'insérer des points de contrôle supplémentaires (afin d'augmenter le nombre d'arcs cubiques pour obtenir une meilleure approximation et au moins assurer la continuité C³ dans les points initiaux, mais pas autour des points de contrôle ajoutés).; L’intérêt des courbes de Bézier de degré 4 ou plus est toutefois plus limité aujourd'hui du fait de l’avancée et de l'intégration du support des B-splines non-uniformes dans les bibliothèques graphiques modernes, et notamment des NURBS, à coefficients rationnels, équivalentes à des B-splines non-uniformes (mais à poids entiers en progression non nécessairement arithmétique, comme c'est le cas des courbes de Bézier), ces B-splines étant cependant calculées d'abord dans un espace projectif à coordonnées homogènes, et qui permettent de conserver l'ensemble des avantages de B-splines de degré 3 ou supérieur, y compris dans le cas des courbes coniques (non linéaires) qui sont impossibles à représenter exactement avec des courbes de Bézier autrement qu'avec une approximation par un grand nombre de sommets et de points de contrôle.

Applications

Animation du tracé d’une courbe de Bézier, avec t à [0,1]
(Cliquez pour voir l'image animée)

Synthèse d'images

Les courbes de Bézier composent l'outil de la base du dessin vectoriel qui repose sur la transcription mathématique des objets.

Les courbes de Bézier cubiques, les plus utilisées, se retrouvent en graphisme et dans de multiples systèmes de synthèse d'images, tels que PostScript, Metafont et The GIMP, pour dessiner des courbes « lisses » joignant des points ou des polygones de Bézier.

Dans le logiciel de dessin matriciel, Paint, il est possible de créer des courbes de Bézier avec l'outil "Courbe". Cela se fait en traçant un trait de P₀ à P₃ puis en cliquant successivement aux lieux de P₁ et P₂.

Les courbes de Bézier cubiques sont également utilisées par les logiciels de dessin vectoriel suivants:
- Dans le logiciel libre jPicEdt il y a un outil pour créer et éditer des chaines de courbes de Bézier d'ordre 3.
- Dans le logiciel libre Inkscape.

Rendus de fontes

Les textes sont également définis par des courbes de Bézier dans le cadre des fonctions de PAO comme la mise en page complexe, la gestion de bloc de texte, les habillages.
Les fontes TrueType utilisent des courbes de Bézier quadratiques plus simples.