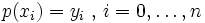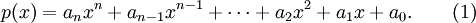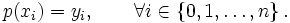- Interpolation Polynomiale
-
Interpolation polynomiale
En mathématiques, en analyse numérique, l' interpolation polynomiale est une technique d'interpolation d'un ensemble de données ou d'une fonction par un polynôme. En d'autres termes, étant donné un ensemble de points (obtenu, par exemple, à la suite d'une expérience), on cherche un polynôme qui passe par tous ces points, et éventuellement vérifie d'autres conditions, de degré si possible le plus bas.
Le résultat n'est toutefois pas toujours à la hauteur des espérances : l'interpolation de Lagrange, par exemple, peut fort bien diverger même pour des fonctions très régulières (Phénomène de Runge).
Sommaire
Définition
- Dans la version la plus simple (interpolation lagrangienne), on impose simplement que le polynôme passe par tous les points donnés. Étant donné un ensemble de n+1 points (xi,yi) (xi distincts 2 à 2), nous devons trouver un polynôme p de degré n au plus qui vérifie :
Le théorème de l'unisolvance précise qu'il n'existe qu'un seul polynôme p de degré n au plus défini par un ensemble de n+1 points.
- L'interpolation d'Hermite consiste à chercher un polynôme qui non seulement prend les valeurs fixées en les abscisses données, mais dont également la dérivée, donc la pente de la courbe, prend une valeur imposée en chacun de ces points. Naturellement, il faut pour cela un polynôme de degré supérieur au polynôme de Lagrange. On peut aussi imposer encore la valeur des dérivées secondes, troisièmes, etc. en chaque point. La démarche de l'interpolation newtonienne utilisant les différences divisées est particulièrement adaptée pour construire ces polynômes.
- Avec la définition choisie dans cet article, l'approximation de Bernstein n'est pas exactement une interpolation.
Construction du polynôme d'interpolation de Lagrange
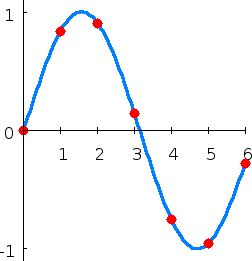 Les points rouges correspondent aux points (xk,yk), et la courbe bleue représente le polynôme d'interpolation.
Les points rouges correspondent aux points (xk,yk), et la courbe bleue représente le polynôme d'interpolation.Supposons que le polynôme d'interpolation est donné par :
Or p doit vérifier :
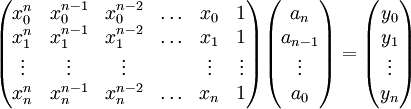
afin que ce dernier passe par l'ensemble des points à interpoler. En intégrant à l'équation (1) , on obtient un système d'équations linéaires d'inconnus ak. L'écriture matricielle est la suivante :
Pour construire p(x), il suffit de résoudre ce système afin d'obtenir les valeurs des ak. Toutefois, inverser une matrice pleine est un calcul lourd (avec une méthode d'élimination de Gauss-Jordan, le calcul est de l'ordre de
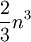 opérations). Des méthodes nettement plus efficaces utilisent une base de polynômes lagrangienne ou newtonnienne pour obtenir une matrice respectivement diagonale ou triangulaire. Dans la pratique, le calcul des différences divisées remplace la résolution du système linéaire.
opérations). Des méthodes nettement plus efficaces utilisent une base de polynômes lagrangienne ou newtonnienne pour obtenir une matrice respectivement diagonale ou triangulaire. Dans la pratique, le calcul des différences divisées remplace la résolution du système linéaire.La matrice est une matrice du type matrice de Vandermonde. Son déterminant est non nul, ce qui prouve le théorème d'unisolvance : le polynôme d'interpolation est unique. (Cela résulte aussi du Théorème fondamental de l'algèbre, car si P et Q sont de degré n et coïncident en n + 1 points, alors P − Q = 0.)
Erreur d'interpolation
L'erreur d'interpolation lors de l'approximation d'une fonction f, c-à-d. lorsque yi = f(xi) dans ce qui précède, est donnée par une formule de type Taylor-Young : Si f est n + 1 fois continûment différentiable sur I = [min(x0,...xn,x),max(x0,...xn,x)] alors
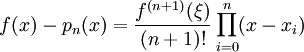 avec
avec 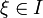 .
.
Cette formule se démontre en appliquant de manière itérée le théorème de Rolle sur les sous-intervalles [xi − 1,...xi].
Dans le cas particulier où xi = x0 + ih (points uniformément répartis), se produit en général une aggravation catastrophique de l'erreur d'interpolation, connue sous le nom de phénomène de Runge, lorsqu'on augmente le nombre de points pour un intervalle [x0,xn] donné.
Voir aussi
- Interpolation lagrangienne
- Interpolation newtonienne
- Interpolation de Bernstein
- (fr) Interpolation polynômiale de type Lagrange.
- (fr) Interpolation polynômiale de type Newton et différences divisées.
Catégorie : Interpolation polynomiale
Wikimedia Foundation. 2010.