Surface de Bezier

Surface de Bezier

Surface de Bézier

Les surfaces de Bézier sont une méthode de définition d'une surface grâce aux courbes de Bézier, avantageuses pour définir une courbe par la donnée de points de contrôle.

Sommaire

Définition

Étant donnée une matrice [M] de points de l'espace Ai,j, la surface de Bézier correspondante est l'ensemble des points M généré par les valeurs comprises entre 0 et 1 des variables u et v du polynôme :

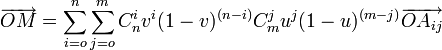
\overrightarrow {O M} = \sum_{i=o}^n \sum_{j=o}^m C_n^i v^i (1-v)^{(n-i)} C_m^j u^j (1-u)^{(m-j)} \overrightarrow {O A_{i j}}

Propriétés

Les points ainsi définis sont évidemment indépendants du choix du point O.
Le cas particulier n = 1 (ou m=1) correspond aux surfaces réglées. Si m = n = 1, on obtient une surface deux fois réglée, qui est soit un plan si les quatre points sont coplanaires, soit un paraboloïde hyperbolique. En considérant sur une telle surface les intersections de deux paires de règles voisines, on se rend compte que la donnée de quatre points ne fait pas que définir la nature de la surface, mais sert aussi à en arrêter les frontières. Dans le cas général, les courbes de Bézier correspondant aux sous-ensembles de points A0,j, An,j, Ai,0, et Ai,m définissent les frontières de la surface.

Voir aussi

Articles connexes

Références

  • (fr) 'Systemes De Cfao', 'Etudes En Cfao Cao Mecanique ','Elements De Cao Volume 1 Materiels Et Logiciels De Base', 'Cao Mécanique', 'Systèmes De C.F.A.O. : Conception Et Fabrication Assistées Par Ordinateur : - Introduction Dans L'entreprise, Méthode De Réalisation ', 'La Cfao - Introduction, Techniques Et Mises En Oeuvre, 3ème Édition Revue Et Corrigée ', 'La Cfao ', de Yvon Gardan, Livres, édition Hermes, (modèles CSG, B-REP, modeleur paramétrique ou variationnel ect...)
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Surface de B%C3%A9zier ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Surface de Bezier de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Surface de bézier — Les surfaces de Bézier sont une méthode de définition d une surface grâce aux courbes de Bézier, avantageuses pour définir une courbe par la donnée de points de contrôle. Sommaire 1 Définition 2 Propriétés 3 Voir aussi …   Wikipédia en Français

  • Surface de Bézier — Les surfaces de Bézier sont une méthode de définition d une surface grâce aux courbes de Bézier, avantageuses pour définir une courbe par la donnée de points de contrôle. Sommaire 1 Définition 2 Propriétés 3 Voir aussi …   Wikipédia en Français

  • Bezier — Bézier Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Pierre Bézier est un ingénieur en mécanique et en électricité français, il est principalement connu pour les courbes de Bézier qui ont trouvé… …   Wikipédia en Français

  • Bézier — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.  Pour l’article homophone, voir Besier. Jean Bezier, chouan ; Pierre Bézier est un ingénieur en mécanique et en électricité français, il est… …   Wikipédia en Français

  • Bézier surface — Bézier surfaces are a species of mathematical spline used in computer graphics, computer aided design, and finite element modelling. As with the Bézier curve, a Bézier surface is defined by a set of control points. Similar to interpolation in… …   Wikipedia

  • Bézier — can refer to:*Pierre Bézier, French engineer and creator of Bézier curves *Bézier curve *Bézier triangle *Bézier spline *Bézier surface * The town of Béziers in France * AS Béziers Hérault, a French rugby union team *Bézier Games, an American… …   Wikipedia

  • Bézier triangle — A cubic Bézier triangle is a surface with the equation:(alpha s+eta t+gamma u)^3 | 0 le s le 1, 0 le t le 1, 0 le u le 1, s+t+u=1:=egin{matrix} eta^3 t^3 + 3alphaeta^2 st^2 + 3eta^2gamma t^2 u + 3alpha^2eta s^2 t + 6alphaetagamma stu +… …   Wikipedia

  • Bézier curve — Cubic Bézier curve A Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case. In… …   Wikipedia

  • Courbe de Bézier — Exemple de construction de courbe de Bézier Les courbes de Bézier sont des courbes polynomiales paramétriques décrites pour la première fois en 1962 par l ingénieur français Pierre Bézier qui les utilisa pour concevoir des pièces d automobiles à… …   Wikipédia en Français

  • Courbe De Bézier — Les courbes de Bézier sont des courbes polynomiales paramétriques décrites pour la première fois en 1962 par l ingénieur français Pierre Bézier qui les utilisa pour concevoir des pièces d automobiles à l aide d ordinateurs. Elles ont de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”