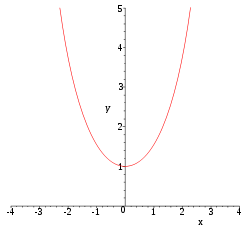
Cosinus hyperbolique

Graphe de la fonction cosinus hyperbolique sur une partie de $\mathbb R$

Le cosinus hyperbolique est, en mathématiques, une fonction hyperbolique.

Sommaire

1 Définition
2 Propriétés
3 Valeurs
4 Zéros
5 Fonction réciproque
6 Utilisation
- 6.1 Physique
- 6.2 Architecture
7 Voir aussi

Définition

La fonction cosinus hyperbolique, notée ch (ou cosh dans les pays Anglo-saxons) est la fonction réelle suivante :

$\begin{matrix} \cosh: &\mathbb R &\longrightarrow &\mathbb R \\ \ &x &\longmapsto &\frac {e^x+e^{-x}} {2} \end{matrix}$

où $x\mapsto e^x$ est la fonction exponentielle.

La fonction cosinus hyperbolique est la partie paire de la fonction exponentielle.

La fonction cosinus hyperbolique est en quelque sorte l'analogue de la fonction cosinus dans la géométrie hyperbolique.

La notation Ch. x a été introduite par Vincenzo Riccati au XVIIIème siècle.

On peut étendre sans problème le cosinus hyperbolique sur $\mathbb{C}$ en utilisant l'exponentielle complexe.

Propriétés

Propriétés générales

cosh est continue et infiniment dérivable, dite de classe $C^\infty$
La dérivée de cosh est sinh, la fonction sinus hyperbolique.
La primitive de cosh est sinh+C, à une constante d'intégration C près.
cosh est paire et strictement croissante sur $\mathbb R^+$ .

Propriétés trigonométriques

De par les définitions des fonctions cosinus et sinus hyperboliques, on peut déduire les égalités suivantes valable pour tout réel x :

$e^x = \cosh(x) + \sinh(x) \,$

$e^{-x} = \cosh(x) - \sinh(x) \,$

Ces égalités sont analogues aux formules d'Euler en trigonométrie circulaire.

De même que le point M de coordonnées (cos(t), sin(t)) parcourt, quand t décrit $\mathbb{R}$ un cercle d'équation $x 2 + y 2 = 1$ , celui de coordonnées (cosh(t), sinh(t)) parcourt une branche d'une hyperbole équilatérale d'équation $x 2 - y 2 = 1$ . On a en effet pour tout réel t :

$\cosh^2(t) - \sinh^2(t) = 1 \,$ .

D'autre part, pour $x \in \mathbb R$ :

$\cosh(i x) = \frac{e^{i x} + e^{-i x}}2= \cos(x)$

$\cosh(x) = \cos(i x) \,$

$\cosh(x+y) = \cosh(x) \cosh(y) + \sinh(x) \sinh(y) \,$

$\cosh^2\left(\frac{x}{2}\right) = \frac{1+\cosh(x)}{2}$

L'utilisation de formules trigonométriques telles que sin(2t) = ^{(2 tan t)}⁄_{(1+tan² t)} permet aussi d'obtenir des relations plus anecdotiques, telle que (pour tout réel $x$ ) :

$\cosh(x)=\frac1{\sin(2\times\arctan(e^x))}$ ;

voir également l'article Gudermannien.

Développement en série de Taylor

cosh, étant indéfiniment dérivable, possède un développement en série de Taylor en tout point :

$\cosh z = 1 + \frac {z^2} {2!} + \frac {z^4} {4!} + \frac {z^6} {6!} + \cdots = \sum_{n=0}^\infty \frac{z^{2n}}{(2n)!}$

Valeurs

Quelques valeurs de cosh :

$\cosh(0) = 1 \,$
$\cosh(1) = \frac {e^2+1}{2e}$
$\cosh(i) = \cos(1) \,$

Zéros

Tous les zéros de $cosh$ sont des imaginaires purs. Plus précisément, pour tout nombre complexe $z$ ,

$\cosh(z)=0 \Leftrightarrow z \in i\pi(\Z+\frac12)~.$

En effet, soit $z = x + i y$ avec $x, y$ réels. On a alors $cosh(z) = cosh(x)cos(y) + i sinh(x)sin(y)$ , donc

$\cosh(z)=0 \Leftrightarrow \cos(y)=0 \mbox{ et } \sinh(x)=0 \Leftrightarrow y \in \{\pi / 2 +k \pi ; k \in \mathbb{Z}\} \mbox{ et } x=0$ .

Fonction réciproque

Graphe de la fonction argument cosinus hyperbolique sur $\left[1;+\infty\right[$

cosh restreinte à $\left[0;+\infty\right[$ est continue et strictement croissante, donc admet une fonction réciproque, notée argcosh (ou argch), et nommée argument cosinus hyperbolique.

Sur $\mathbb{C}$ , il s'agit d'une fonction multivaluée complexe. Sa branche principale est généralement choisie en posant comme coupure le segment $\left]-\infty;1\right[$ .

$\operatorname{argcosh}(z) = \ln(z + \sqrt{z+1} \sqrt {z-1})$

Pour $x \in \left[1;+\infty\right[$ , il existe deux réels dont le cosh vaut $x$ :

$\operatorname{argcosh}(x)=\ln\left(x+\sqrt{x^2-1}\right)$ et

$-\operatorname{argcosh}(x)=\ln\left(x-\sqrt{x^2-1}\right)~.$

En effet, en posant $t=\operatorname{argcosh}(x)$ et en utilisant que $cosh 2 t - sinh 2 t = 1$ et $t > 0$ , on obtient $e^t=\cosh t+\sinh t= x+\sqrt {x^2-1}$ .

Utilisation

Physique

La courbe représentative de la fonction cosh sur $\mathbb R$ décrit une chaînette, c’est-à-dire la forme d'un câble fixé aux deux extrémités et soumis à la pesanteur.

Architecture

Le cosinus hyperbolique correspond en architecture à l'arc caténaire issu au départ de l'ingénierie des ponts suspendus. Antoni Gaudí a été l'un des premiers à l'utiliser massivement en architecture commune avec en particulier deux de ses œuvres les plus connues : la Crypte de la Colonia Güell et la Sagrada Família.

L'arche du Gateway

L'arche du Gateway à Saint-Louis (Missouri) possède la forme d'une chaînette renversée. Elle s'élève à 192 m en son centre et enjambe 192 m à sa base. Les points de cette arche satisfont approximativement l'équation

$y=-39 \cosh \left( \frac{x}{39} \right)+231$

pour -96 < x < 96.

Voir aussi

Sur les autres projets Wikimedia :

« la fonction cosinus hyperbolique », sur Wikimedia Commons (ressources multimédia)

Sur les autres projets Wikimedia :

« la fonction argcosinus hyperbolique », sur Wikimedia Commons (ressources multimédia)

Portail de l'analyse

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cosinus hyperbolique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Cosinus Hyperbolique — Graphe de la fonction cosinus hyperbolique sur une partie de Le cosinus hyperbolique est, en mathématiques, une fonction hyperbolique. Sommaire … Wikipédia en Français
Cosinus Hyperbolique Réciproque — Le cosinus hyperbolique réciproque est, en mathématiques, une fonction hyperbolique. Définition La fonction cosinus hyperbolique réciproque, notée Argch (ou arccosh) est la fonction suivante : Voir aussi Fonction hyperbolique Ce document… … Wikipédia en Français
Cosinus hyperbolique reciproque — Cosinus hyperbolique réciproque Le cosinus hyperbolique réciproque est, en mathématiques, une fonction hyperbolique. Définition La fonction cosinus hyperbolique réciproque, notée Argch (ou arccosh) est la fonction suivante : Voir aussi… … Wikipédia en Français
Cosinus hyperbolique d'un réel x — ● Cosinus hyperbolique d un réel x réel noté ch x égal à … Encyclopédie Universelle
Cosinus hyperbolique réciproque — Le cosinus hyperbolique réciproque est, en mathématiques, une fonction hyperbolique. Définition La fonction cosinus hyperbolique réciproque, notée Argch (ou arccosh) est la fonction suivante … Wikipédia en Français
Fonction cosinus hyperbolique — ● Fonction cosinus hyperbolique fonction définie sur R : x ↦ ch x … Encyclopédie Universelle
cosinus — [ kɔsinys ] n. m. • co sinus 1717; de co et sinus ♦ Fonction trigonométrique faisant correspondre à l angle de deux axes la mesure de la projection orthogonale sur l un, d un vecteur unitaire porté par l autre; sinus de l angle complémentaire.… … Encyclopédie Universelle
hyperbolique — [ ipɛrbɔlik ] adj. • 1541; lat. hyperbolicus, gr. huperbolikos I ♦ Rhét. Caractérisé par l hyperbole. Style hyperbolique. Cour. Des compliments hyperboliques. ⇒ emphatique, grandiloquent. Philos. Le doute hyperbolique (Descartes). II ♦ (1646) 1 ♦ … Encyclopédie Universelle
Cosinus (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Hyperbolique — Fonction hyperbolique En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Cosinus hyperbolique

Sommaire

Définition