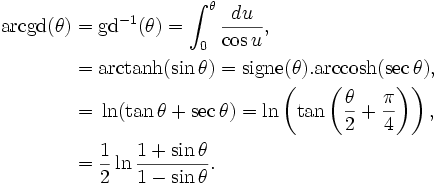Gudermannien

Gudermannien

Fonction de Gudermann

En mathématiques, la fonction de Gudermann, appelée aussi parfois gudermannien, et notée gd, nommée en l'honneur de Christoph Gudermann (1798 - 1852), fait le lien entre la trigonométrie circulaire et la trigonométrie hyperbolique sans faire intervenir les nombres complexes.

Sommaire

Définition

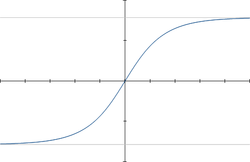
(Fonction de Gudermann avec son asymptote (en gris) : \scriptstyle{\theta=\pm\frac{\pi}{2}}\,\!.

La fonction de Gudermann est définie sur l'ensemble des réels par :

\begin{align}{\rm{gd }} (t) &=\int_0^t\frac{du}{\cosh u}\\ &=\arcsin\left(\tanh t\right)=\mbox{signe}(t).\arccos\left(\mbox{sech } t\right)\ \\ &=\arctan\left(\sinh t\right)=\mbox{signe}(t).\mbox{arcsec}\left(\cosh t\right)\\ &=\mbox{arccot}\left(\mbox{csch } t\right)=\mbox{arccsc}\left(\coth t\right)\\ &=2\arctan\left(\tanh\frac{t}{2}\right)=2\arctan e^t-\frac{\pi}{2}.\end{align}\,\!

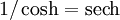La dérivée de la fonction de Gudermann est la fonction 1/\cosh =\mbox{sech} \!.

Le réel 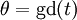\theta= \mbox{gd} (t) \!, appelé parfois gudermannien de 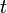t \!, est relié à ce dernier par les relations :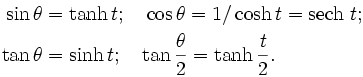

\begin{align}{\color{white}\dot{{\color{black}\sin \theta}}}&=\tanh t;\quad\cos\theta =1/\cosh t=\mbox{sech } t ;\\ \tan \theta&=\sinh t;\quad\tan\frac{\theta}{2}=\tanh\frac{t}{2}.\end{align}\,\!

Fonction inverse

La fonction de Gudermann inverse est définie sur ]-\pi/2,\pi/2[\! par :

\begin{align} \mbox{arcgd}(\theta)&={\rm {gd}}^{-1}(\theta)=\int_0^\theta\frac{du}{\cos u},\\ &=\mbox{arctanh}(\sin \theta)=\mbox{signe}(\theta){.}\mbox{arccosh}(\sec \theta),\\ &={}\ln(\tan \theta+\sec \theta)=\ln\left(\tan\left(\frac{\theta}{2}+\frac{\pi}{4}\right)\right),\\ &={}\frac{1}{2}\ln \frac{1+\sin \theta}{1-\sin \theta} .\end{align}\,\!

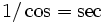La dérivée de la fonction de Gudermann inverse est la fonction 1/\cos =\mbox{sec} \!.

Applications

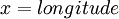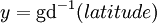  • Les cordonnées de Mercator d'un point de la sphère sont définies par x=longitude\! et y=\mbox{gd}^{-1}(latitude)\!.

Elles sont ainsi définies de sorte que les loxodromies de la sphère soient représentées par des droites dans le plan x,y\!.

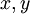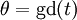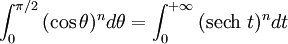  • Le changement de variable \theta=\mbox{gd}(t)\! permet de transformer des intégrales de fonctions circulaires en intégrales de fonctions hyperboliques ; par exemple, \int_0^{\pi/2}{(\cos \theta)^n d\theta} = \int_0^{+\infty}{(\mbox{sech } t)^n dt}.
  • Ceci explique pourquoi on peut choisir des fonctions circulaires ou hyperboliques lors de changement de variables dans le calcul d'intégrales :

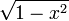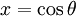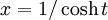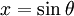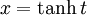Quand on rencontre du \sqrt{1-x^2}, on utilise x=\cos\theta\! ou x=1/\cosh t\!, et on utilise aussi x=\sin\theta\! ou x=\tanh t\!.

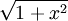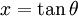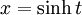Quand on rencontre du \sqrt{1+x^2}, on utilise x=\tan\theta\! ou x=\sinh t\!.

  • Paramétrisation d'un cercle ou d'une droite hyperbolique.

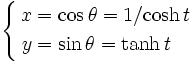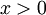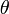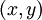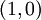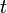Si on pose \begin{cases}\begin{align}x&= \cos \theta = 1/{\cosh t} \\ y & = \sin \theta = \tanh t \end{align}\end{cases}, on a évidemment une paramétrisation du demi-cercle de rayon 1 dans le demi-plan x>0\! ; \theta\! est la distance curviligne dans le demi-plan euclidien entre le point (x,y)\! et le point (1,0)\!, et t\! est aussi une distance, mais mesurée entre ces deux points dans le demi-plan considéré comme demi-plan de Poincaré pour la géométrie hyperbolique.

Voir aussi

Références

  • CRC Handbook of Mathematical Sciences 5th ed. pp 323-5.
  • (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Gudermannian function ».
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction de Gudermann ».

Wikimedia Foundation. 2010.

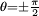Contenu soumis à la licence CC-BY-SA. Source : Article Gudermannien de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Fonction De Gudermann — En mathématiques, la fonction de Gudermann, appelée aussi parfois gudermannien, et notée gd, nommée en l honneur de Christoph Gudermann (1798 1852), fait le lien entre la trigonométrie circulaire et la trigonométrie hyperbolique sans faire… …   Wikipédia en Français

  • Fonction de Gudermann — En mathématiques, la fonction de Gudermann, appelée aussi parfois gudermannien, et notée gd, nommée en l honneur de Christoph Gudermann (en) (1798 1852), fait le lien entre la trigonométrie circulaire et la trigonométrie hyperbolique sans… …   Wikipédia en Français

  • Fonction de gudermann — En mathématiques, la fonction de Gudermann, appelée aussi parfois gudermannien, et notée gd, nommée en l honneur de Christoph Gudermann (1798 1852), fait le lien entre la trigonométrie circulaire et la trigonométrie hyperbolique sans faire… …   Wikipédia en Français

  • Cosinus hyperbolique — Graphe de la fonction cosinus hyperbolique sur une partie de Le cosinus hyperbolique est, en mathématiques, une fonction hyperbolique. Sommaire …   Wikipédia en Français

  • Projection de Mercator — Planisphère du monde selon la projection de Mercator. La projection …   Wikipédia en Français

  • Sinus hyperbolique — Graphe de la fonction sinus hyperbolique sur une partie de Le sinus hyperbolique est, en mathématiques, une fonction hyperbolique. Sommaire …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”