Corps Global
- Corps Global
-
Corps global
En mathématiques, le terme corps global fait référence à une des définitions suivantes :
Il existe de nombreuses similarités formelles entre ces deux types de corps. Un corps de l'un ou de l'autre type possède la propriété que toutes ses complétions sont des corps localement compacts (voir corps locaux). Chaque corps de l'un ou de l'autre type peut être vu comme le corps quotient d'un anneau de Dedekind dans lequel chaque idéal différent de zéro est d'indice fini. Dans chaque cas, on a la formule produit pour les éléments différents de zéro x :
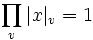 .
.
L'analogie entre ces deux approches a été source d'une grande motivation pour la théorie algébrique des nombres. En particulier, il est généralement plus facile de travailler dans le cas des corps de fonction puis d'essayer de développer des techniques similaires du côté des corps de nombres. Le développement de la théorie d'Arakelov et son exploitation par Gerd Faltings dans sa démonstration de la conjecture de Mordell est un exemple spectaculaire.
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorie des corps | Géométrie arithmétique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Corps Global de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Corps global — En mathématiques, le terme corps global est un corps d un des types suivants : un corps de nombres, c est à dire une extension finie de un corps de fonction d une courbe algébrique sur un corps fini, c est à dire une extension finie du corps … Wikipédia en Français
Corps De Nombres — En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la forme où α est… … Wikipédia en Français
Corps De Nombres Algébriques — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la … Wikipédia en Français
Corps de nombre — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la … Wikipédia en Français
Corps de nombres algebriques — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la … Wikipédia en Français
Corps de nombres algébriques — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la … Wikipédia en Français
Corps des nombres algébriques — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la … Wikipédia en Français
Corps de nombres — Ne pas confondre avec la notion d ensemble de nombres. En mathématiques, un corps de nombres est une extension finie du corps des nombres rationnels. En particulier, c est une extension algébrique : tous les éléments de K sont des… … Wikipédia en Français
Corps de fonctions — En mathématiques, un corps de fonctions est un corps de type fini sur un corps de base. Définition Soit k un corps commutatif. Un corps de fonctions F sur k est un corps de type fini sur k. De façon équivalente, c est une extension finie d un… … Wikipédia en Français
Global garden — Le dernier rêve d Einstein GLOBAL GARDEN アインシュタイン睡夢奇譚 (Gurōbaru gāden ainshutain suimu kitan) Type Shōjo Genre mystère, science fiction Manga Auteur Saki Hiwatari Éditeur … Wikipédia en Français
 .
.