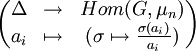Extension de Kummer

En mathématiques, la théorie de Kummer, ainsi désignée suivant le nom du mathématicien allemand du XIX siècle Ernst Kummer, suite à ses travaux sur le dernier théorème de Fermat, donne une description de certaines extensions d'un corps contenant suffisamment de racines de l'unité.

Extension de Kummer

Soit un corps commutatif K contenant les racines n-èmes de l'unité, pour n un nombre entier premier à la caractéristique de K si elle est positive. Une extension L/K est de Kummer si le corps L est K-engendré par une racine d'un polynôme Xⁿ-a à coefficients dans K.

Par exemple, en caractéristique différente de 2, l'expression des racines des trinômes du second degré montre que toute extension quadratique est une extension de Kummer. En revanche, en caractéristique 2, il n'y a pas d'extension de Kummer de degré 2.

Si le corps K ne contient aucune racine m-ème de a, pour m>1 divisant n, l'extension de Kummer de K donnée par les racines du polynôme Xⁿ-a est une extension galoisienne, de groupe de Galois cyclique d'ordre n, dont un générateur σ est défini par son action sur une racine n-ème de a :

où ζ_n désigne une racine primitive n-ème de l'unité. Sans hypothèse sur les racines de a dans K, l'extension est cyclique d'ordre divisant n.

Plus généralement, on parle d'extension de Kummer pour un compositum d'un nombre fini d'extensions de Kummer élémentaires telles que décites ci-dessus, c'est-à-dire obtenues en adjoignant les racines n-èmes de l'unité d'un nombre fini d'éléments a_i du corps K. Un telle extension est à nouveau galoisienne, et son groupe de Galois est produit direct de groupes cycliques d'ordre divisant n, elle est donc abélienne, et son groupe de Galois a un exposant qui divise n.

Théorie de Kummer

La théorie de Kummer traite les réciproques, c'est-à-dire la question : dans quelle mesure les extensions abéliennes d'un corps peuvent-elles être décrites à l'aide de racines n-èmes d'éléments de ce corps ?

Une réponse est donnée par l'énoncé : si K est un corps contenant les racines n-èmes de l'unité, pour n un entier que ne divise pas la caractéristique de K, et si L est une extension abélienne finie de K, dont le groupe de Galois est d'exposant divisant n, alors il existe des éléments a₁,...,a_r de K tels que . Les éléments a₁, ..., a_r engendrent un sous-groupe abélien Δ, d'exposant divisant n, du groupe quotient K^*/(K^*)ⁿ. Il y a donc une correspondance entre de tels sous-groupes Δ et les extensions abéliennes de K de groupe de Galois G d'exposant divisant n, et il existe un isomorphisme :

En notant n_i le plus grand entier divisant n tel que la racine n_i-ème de a soit dans K, il existe donc une famille d'éléments σ_i du groupe G qui laissent fixes les a_j pour j différent de i, et agissent sur a_i par multiplication par .

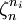Voir aussi

Dans le cas d'une extension abélienne d'ordre p, d'un corps commutatif de caractéristique p, voir : théorie d'Artin-Schreier.

Référence

(en) Jürgen Neukirch, Algebraic number theory [détail des éditions]

• Portail des mathématiques