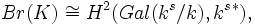Groupe De Brauer

Groupe De Brauer

Groupe de Brauer

En mathématiques, le groupe de Brauer constitue l'espace classifiant des algèbres centrales simples sur un corps commutatif k donné, pour une certaine relation d'équivalence. On munit cet espace d'une structure de groupe abélien en l'identifiant à un espace de cohomologie galoisienne.

Sommaire

Construction du groupe de Brauer

Une algèbre centrale simple sur un corps commutatif k, est une algèbre associative de dimension finie A, qui n'admet aucun idéal bilatère non trivial (simplicité), et dont le centre est k (centralité). Par exemple, le corps des nombres complexes forme une algèbre centrale simple sur lui-même, mais pas sur le corps des nombres réels, la propriété de centralité étant en défaut. En revanche, l'algèbre des quaternions d'Hamilton est une algèbre centrale simple sur le corps des nombres réels.

Étant données deux algèbres centrales simples A et B, on définit le produit tensoriel 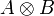A\otimes B à partir du produit tensoriel d'espaces vectorielspris comme des espaces vectoriels en ajoutant la propriété de bilinéarité : 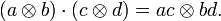(a \otimes b) \cdot (c\otimes d) = ac\otimes bd. Un produit tensoriel de deux algèbres centrales simples est une algèbre centrale simple.

La première caractérisation importante des algèbres centrales simples est que ce sont exactement les algèbres A de dimension finie qui deviennent isomorphes à une algèbre de matrices Mn(K) par extension des scalaires à une extension finie K du corps k ; c'est-à-dire en considérant le produit tensoriel A\otimes_k K\simeq M_n(K). Par ailleurs, le théorème de Wedderburn assure que toute algèbre simple est isomorphe à une algèbre de matrices à coefficients dans un corps (non commutatif) D contenant k, le corps D étant unique à isomorphisme près. On introduit alors la relation suivante : deux algèbres centrales simples A et A' sont équivalentes si et seulement si le même corps D peut être choisi pour les deux dans ce qui précède. 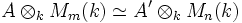Une autre définition équivalente consiste à demander qu'il existe des entiers m et n tels qu'on ait un isomorphisme d'algèbres A\otimes_k M_m(k)\simeq A'\otimes_k M_n(k).

Les classes d'équivalence pour cette relation forment alors un groupe abélien pour le produit tensoriel appelé groupe de Brauer. L'opposé d'une classe d'équivalence dont un représentant est A est la classe d'équivalence de l'algèbre opposée Aop (définie en changeant l'opération de multiplication . par la relation * définie par : a*b=b.a) ; ceci se montre par le fait que le morphisme qui à 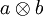a\otimes b associe le k-endomorphisme sur A qui à x associe axb définit un isomorphisme entre le produit tensoriel 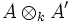A\otimes_k A' et un espace de k-endomorphismes, c'est-à-dire un espace de matrices à coefficients dans k, donc trivial dans le groupe de Brauer.

Exemples

Le groupe de Brauer d'un corps algébriquement clos (toutes les algèbres centrales simples sont isomorphes à une algèbre de matrices) ou d'un corps fini (les corps contenant un corps fini, et de dimension finie sur celui-ci sont finis donc commutatifs par un autre théorème de Wedderburn) est le groupe trivial.

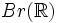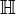Le groupe de Brauer Br(\mathbb{R}) du corps des nombres réels \mathbb{R} est un groupe cyclique d'ordre deux : il existe seulement deux types de corps contenant celui des nombres réels et central sur celui-ci, à savoir \mathbb{R} lui-même et l'algèbre des quaternions \mathbb{H}\,. Le produit dans le groupe de Brauer est basé sur le produit tensoriel : l'énoncé que 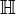\mathbb{H}\, est d'ordre deux dans le groupe de Brauer est équivalent à l'existence d'un isomorphisme de \mathbb{R}-algèbres

\mathbb{H} \otimes \mathbb{H} \cong M(4, \mathbb{R})

d'algèbres à 16 dimensions.

Généralisation

Les groupes de Brauer des corps locaux peuvent être calculés ; ils sont tous canoniquement isomorphes à 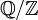\mathbb{Q} / \mathbb{Z}\,, pour les corps de nombres p-adiques. Les résultats sont ensuite appliqués aux corps globaux, c'est l'approche cohomologique de la théorie des corps de classes. Plus précisément, le groupe de Brauer Br(K) d'un corps global K est donné par la suite exacte

0\rightarrow Br(K)\rightarrow \oplus_p Br(K_p)\rightarrow \mathbb{Q} / \mathbb{Z} \rightarrow 0

où la somme du milieu porte sur toutes les complétions (archimédiennes et non-archimédiennes) de K. Le groupe 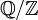\mathbb{Q} / \mathbb{Z}\, sur la droite est en fait le "groupe de Brauer" de la formation de classes des classes d'idèles associées à K.

Dans la théorie générale, le groupe de Brauer est exprimé par des groupes de cohomologie :

Br(K) \cong H^2(Gal(k^s/k), {k^s}^*),

où ks est la clôture séparable du corps k.

Une généralisation en géométrie algébrique, due à Grothendieck, constitue la théorie des algèbres d'Azumaya.

Voir aussi

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Groupe de Brauer ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Groupe De Brauer de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Groupe de brauer — En mathématiques, le groupe de Brauer constitue l espace classifiant des algèbres centrales simples sur un corps commutatif k donné, pour une certaine relation d équivalence. On munit cet espace d une structure de groupe abélien en l identifiant… …   Wikipédia en Français

  • Groupe de Brauer — En mathématiques, le groupe de Brauer constitue l espace classifiant des algèbres centrales simples sur un corps commutatif k donné, pour une certaine relation d équivalence. On munit cet espace d une structure de groupe abélien en l identifiant… …   Wikipédia en Français

  • BRAUER (R.) — BRAUER RICHARD (1901 1977) Mathématicien américain d’origine allemande dont les travaux ont porté principalement sur la théorie des groupes finis. Né à Berlin, Brauer a enseigné à l’université de Koenigsberg, à celle de Toronto (Mi.) et à… …   Encyclopédie Universelle

  • Groupe (mathématique) — Groupe (mathématiques) Pour les articles homonymes, voir Groupe.  Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes …   Wikipédia en Français

  • Groupe (mathématiques) — Pour les articles homonymes, voir Groupe. Les manipulations possibles du cube de Rubik forment un groupe. En mathématiques, un groupe est un ensemble …   Wikipédia en Français

  • Richard Brauer — Pour les articles homonymes, voir Brauer. Richard et Ilse Brauer en 1970 Richard Dagobert Brauer (10 février 1901 à Berlin – 17 avril 1977 à Belmont (Massachusetts)  …   Wikipédia en Français

  • Richard Dagobert Brauer — Richard Brauer Pour les articles homonymes, voir Brauer. Richard Dagobert Brauer (10 février, 1901 à Berlin 17 avril, 1977 à Belmont, Massachusetts) était un mathématicien allemand et américain. Il a surtout travaillé en algèbre, mais a aussi… …   Wikipédia en Français

  • Structure de groupe — Groupe (mathématiques) Pour les articles homonymes, voir Groupe.  Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes …   Wikipédia en Français

  • Théorie de Groupe — Groupe (mathématiques) Pour les articles homonymes, voir Groupe.  Cet article concerne une introduction au concept de groupe. Pour un approfondissement, voir théorie des groupes …   Wikipédia en Français

  • Representations d'un groupe fini — Représentations d un groupe fini En mathématiques, un groupe est une structure algébrique dont la définition est remarquablement simple. Elle consiste en un ensemble muni d une unique opération. Cette opération possède de bonnes propriétés, elle… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”