- Carré
-
Pour les articles homonymes, voir Carré (homonymie).
Un carré.
Un carré est un polygone régulier à quatre côtés. Cela signifie que ses quatre côtés ont la même longueur et ses quatre angles la même mesure. Un carré est à la fois un rectangle et un losange.
Le carré possède de nombreuses propriétés de symétrie et de régularité. Tout carré a quatre axes de symétrie et est invariant par des rotations d'angle droit. Deux côtés consécutifs d'un carré sont perpendiculaires, de même que ses diagonales. Ces propriétés sont connues depuis la plus haute Antiquité. Les premières représentations du carré datent de la préhistoire. Il est, avec le cercle, l'une des figures géométriques remarquables les plus étudiées depuis l'Antiquité, le problème de la quadrature du cercle ayant tenu en haleine de nombreux mathématiciens pendant deux millénaires.
Le « carré d'un nombre » désigne également le produit de ce nombre par lui-même. Il est noté a × a = a2 et se lit « a au carré » ou « a carré ». Cette expression s'est imposée durant la période où l'algèbre géométrique était omniprésente, le carré d'un nombre étant vu comme la surface d'un carré de côté le nombre initial.
Sommaire
Propriétés
Un carré est à la fois un losange et un rectangle, il possède donc les propriétés de ces deux quadrilatères. Il peut également être vu comme un polygone régulier, ce qui permet de démontrer ses propriétés par déduction de celles de ces polygones.
Angles et côtés
Un carré possède quatre angles droits (comme tout un rectangle) et tous ses côtés ont la même longueur (il est un losange). Les côtés opposés d'un carré sont parallèles deux à deux, ce qui en fait un cas particulier de parallélogramme.
Diagonales
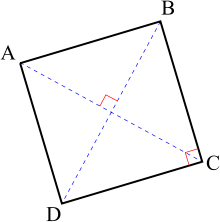
Un carré noté ABCD avec ses diagonales.Comme parallélogramme particulier, tout carré possède des diagonales qui se coupent en leur milieu. Ce point d'intersection est appelé le centre du carré. Notons-le O. Les diagonales de tout rectangle — et donc de tout carré — ont la même longueur. Donc il existe un cercle de centre O passant par les quatre sommets du carré. Le rayon de ce cercle est égal à la longueur d'une demi-diagonale.
Les diagonales de tout carré sont perpendiculaires, comme celles de tout losange.
Chaque diagonale partage le carré en deux triangles qui sont à la fois rectangles et isocèles. Les deux diagonales ensembles délimitent dans le carré quatre triangles rectangles isocèles.
Mesures
Tous les carrés sont semblables. Cela signifie que, pour deux carrés donnés, il existe toujours un agrandissement (ou une réduction) permettant de transformer l'un en l'autre en conservant les angles géométriques et les proportions. On peut donc définir entièrement un carré par la longueur c de ses côtés.
L'aire d'un carré est c×c = c2. Son périmètre mesure 4c et chaque diagonale mesure c√2.
Le carré est, parmi les quadrilatères de même périmètre, celui qui possède la plus grande surface. Cette figure est la réponse à la question d'isopérimétrie dans les quadrilatères.
Dimensions d'un carré de côté c et de diagonale d Diagonale 
Côté 
Périmètre 
Aire 
Symétries
Les transformations laissant un carré invariant sont de deux types :
- les symétries axiales, dont l'axe est soit une diagonale du carré, soit une médiatrice d'un côté ;
- les rotations dont le centre est le centre du carré et dont l'angle est un multiple de l'angle droit.
En voici la liste, elles sont au nombre de huit et forment un groupe :
id (identité : chaque point est conservé)
r1 (rotation de 90° vers la droite)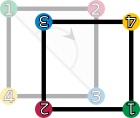
r2 (rotation de 180°)
r3 (rotation de 270° vers la droite)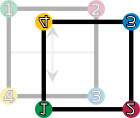
fv (retournement vertical)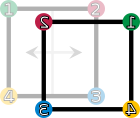
fh (retournement horizontal)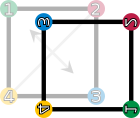
fd (retournement suivant la première diagonale)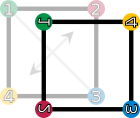
fc (retournement suivant la deuxième diagonale)Les éléments du groupe de symétrie (D4). Les sommets sont colorés et numérotés uniquement pour visualiser les transformations. Toute droite passant par O divise le carré en deux parties superposables.
Construction au compas seul
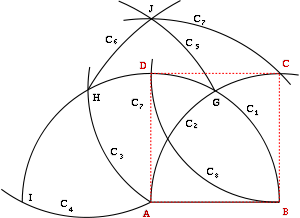
On souhaite construire le carré de sommets ABCD connaissant seulement les points A et B. Posons R la distance entre A et B ; alors, on procède comme suit :
- on trace C1 le cercle de centre A et de rayon R (qui contient alors B)
⇒ on a un troisième point du carré sur ce cercle ; - on trace C2 le cercle de centre B et de rayon R (qui contient alors A)
⇒ le quatrième point du carré, C, se trouve sur ce cercle ; - Posons G un point d'intersection de C1 avec C2 ; on construit alors le point I, symétrique de B par rapport à A :
- on trace C3 centré en G et de rayon R ; ce cercle coupe C1 en B et en un autre point H,
- C4, de centre H et de rayon R, coupe C1 en G et en un nouveau point I ;
- posons S la distance entre G et I ; on construit alors C5 de centre I et de rayon S (il contient forcément G) ;
- C6 s'obtient en prenant pour centre B et pour rayon S (il contient forcément H) ; on note J le point d'intersection entre C6 et C5 qui est du même côté que G par rapport à la droite (AB) ;
- si T est la distance entre A et J, on construit C7 le cercle de centre A et de rayon T (il contient forcément J)
⇒ Le point C est obtenu par intersection entre C7 et C2 ; - on construit alors C8 de centre C et de rayon R
⇒ l'intersection de C8 et C1 est le point D.
Histoire
La tablette d'argile YBC 7289 : une très ancienne (environ 1700 avant J.-C.) représentation d'un carré avec ses diagonales et une valeur approchée de √2 (crédits : Bill Casselman).Des poteries décorées de carrés sont attestées dès le VIe millénaire av. J.‑C. en Mésopotamie[1].
Des tablettes démontrent la connaissance des symétries et rotations du carré vers le XVIIIe siècle av. J.‑C.. La tablette BM 15285 contient une quarantaine de problèmes mathématiques concernant des aires de figures liées à des carrés[1].
Le Talmud recommande de bâtir des villes de forme carrée, quelle que soit la forme de son enceinte[2].
Annexes
Bibliographie
- (en) Eleanor Robson, Mathematics in Ancient Iraq: a Social History, Princeton University Press, 2008, 442 p. (ISBN 9780691091822)
Voir aussi
Notes
- Eleanor Robson 2008
- Salomon Munk, Tanchum ben Joseph, Leopold Dukes, Isidore Cahen, La Bible: traduction nouvelle, 1833
Wikimedia Foundation. 2010.
