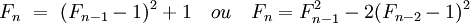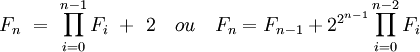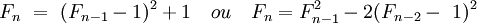4294967297

4294967297

Nombre de Fermat

Pierre de Fermat étudie les propriétés des nombres portant maintenant son nom.

Un nombre de Fermat est un entier naturel qui peut s'écrire sous la forme 22n + 1, avec n entier. Le ne nombre de Fermat, 22n + 1, est noté Fn.

Ces nombres doivent leur nom au mathématicien français Pierre de Fermat (1601-1665) qui émit la conjecture que tous ces nombres étaient premiers. Cette conjecture se révéla fausse, F5 étant composé, de même que tous les nombres de Fermat jusqu'à F32. Les seuls nombres de Fermat premiers connus sont donc F0, F1, F2, F3 et F4, et on ne sait pas si les nombres à partir de F33 sont premiers ou composés.

Ces nombres disposent de propriétés intéressantes, en général issues de l'arithmétique modulaire ; en particulier, Carl Friedrich Gauss a établi un lien entre ces nombres et la construction à la règle et au compas des polygones réguliers : un polygone régulier à n côtés peut être construit à la règle et au compas si et seulement si n est une puissance de 2, ou le produit d'une puissance de 2 et de nombres de Fermat premiers distincts.

Sommaire

Histoire

En 1640, dans une lettre adressée à Bernard Frénicle de Bessy (1605 - 1675), Pierre de Fermat énonce, et probablement démontre son petit théorème : « Et cette proposition est généralement vraie en toutes progressions et en tous nombres premiers ; de quoi je vous envoierois la démonstration, si je n'appréhendois d'être trop long »[1]. Ce théorème lui permet d'étudier les nombres portant maintenant son nom. Dans cette même lettre[2], il émet la conjecture que ces nombres sont tous premiers sans parvenir à trouver une preuve « ... je n'ai pu encore démontrer nécessairement la vérité de cette proposition ». Cette hypothèse le fascine, deux mois plus tard, dans une lettre à Marin Mersenne (1588 - 1648), il écrit : « Si je puis une fois tenir la raison fondamentale que 3, 5, 7, 17, 257, 65537... sont nombres premiers, il me semble que je trouverai de très belles choses en cette matière, car j'ai déjà trouvé des choses merveilleuses dont je vous ferai part »[3]. Il écrit encore à Blaise Pascal (1623 - 1662) : « je ne vous demanderais pas de travailler à cette question si j'avais pu la résoudre moi-même ». Dans une lettre à K. Digby, non datée mais envoyée par Digby à Wallis le 16 juin 1658, Fermat donne encore sa conjecture [4] comme non démontrée[5]. Toutefois, dans une lettre de 1659 à Caracavi[6], il s'exprime en des termes qui, selon certains auteurs, impliquent qu'il estime avoir trouvé une démonstration[7].

Cette conjecture se révèlera fausse, c'est d'ailleurs la seule conjecture erronée de Fermat. Leonhard Euler (1707 - 1783) présente[8] un diviseur de F5 en 1732. Il ne dévoile la construction de sa preuve[9] que quinze ans plus tard. Elle correspond exactement aux travaux de Fermat lui ayant permis de démontrer[10] en 1640 la non primalité des candidats de paramètres 23 et 37 pour les nombres de Mersenne.

Propriétés

Premières propriétés

La suite des nombres de Fermat possède plusieurs relations de récurrence. On peut citer par exemple si n est supérieur ou égal à deux :

  • F_n \ = \ (F_{n - 1} -1)^2 + 1 \quad ou \quad F_{n} = F_{n-1}^2 - 2(F_{n-2}-1)^2\;

Où encore, avec des produits de nombres de Fermat :

  • F_n \ = \ \prod_{i=0}^{n-1} F_i \ + \ 2 \quad ou \quad F_{n} = F_{n-1} + 2^{2^{n-1}}\prod_{i=0}^{n-2} F_i\;

On en déduit le théorème de Goldbach[11] affirmant que :

Soit D(n, b) le nombre de chiffres utilisés pour écrire Fn en base b.

  • La valeur de D(n,b) est donnée par la formule suivante :
D(n,b) = \lfloor \log_{b}\left(2^{2^{\overset{n}{}}}+1\right)+1 \rfloor \approx \lfloor 2^{n}\,\log_{b}2+1 \rfloor

Les crochets désignent la fonction partie entière et logb le logarithme de base b.

  • Aucun nombre de Fermat n'est somme de deux nombres premiers à l'exception de F1 = 2 + 3.
  • Aucun nombre de Fermat n'est la différence de deux puissances de nombres premiers impairs.
  • La somme des inverses de tous les nombres de Fermat est irrationnelle.[12]


Démonstrations
  • F_n \ = \ (F_{n - 1} -1)^2 + 1 \quad ou \quad F_{n} = F_{n-1}^2 - 2(F_{n-2}-\ 1)^2\;

En effet:

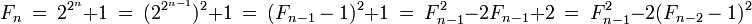
F_n \ = \ 2^{2^n} + 1 \ = \ (2^{2^{n-1}})^2 + 1 \ = \ (F_{n-1} \ - \ 1)^2 + 1 \ = \ F_{n-1}^2 - 2F_{n-1} + 2 \ = \ F_{n-1}^2 - 2(F_{n-2}\ -\ 1)^2
  • F_n \ = \ \prod_{i=0}^{n-1} F_i \ + \ 2 \quad ou \quad F_{n} = F_{n-1} + 2^{2^{n-1}}\prod_{i=0}^{n-2} F_i\;

Une récurrence et l'égalité suivante permet de calculer le premier produit :

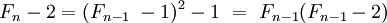
F_n - 2 = (F_{n-1} \ - 1)^2 - 1 \ = \ F_{n-1}(F_{n-1} -2) \;

La seconde égalité s'en déduit :

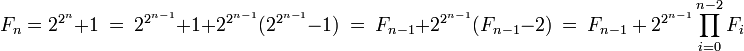
F_n = 2^{2^n} + 1 \ = \ 2^{2^{n-1}} + 1 + 2^{2^{n-1}}(2^{2^{n-1}} -1) \ = \ F_{n-1} + 2^{2^{n-1}}(F_{n-1} - 2) \ = \ F_{n-1} \ + \ 2^{2^{n-1}}\prod_{i=0}^{n-2} F_i
  • Deux nombres de Fermat distincts sont premiers entre eux.

Soit n et m deux entiers positifs tel que n est strictement plus grand que m. Montrons que le seul facteur commun à Fn et Fm et un. Un calcul précédent montre que :

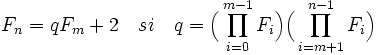
F_n = qF_m + 2 \quad si \quad q = \Big( \prod_{i=0}^{m-1} F_i \Big)\Big( \prod_{i=m+1}^{n-1} F_i \Big)

Donc un diviseur commun à Fn et Fm est aussi un diviseur de deux. Or deux ne divise pas Fn, ces trois entiers sont donc premiers entre eux deux à deux.

  • La valeur de D(n,b) est donnée par la formule suivante :
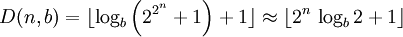
D(n,b) = \lfloor \log_{b}\left(2^{2^{\overset{n}{}}}+1\right)+1 \rfloor \approx \lfloor 2^{n}\,\log_{b}2+1 \rfloor

Il suffit de remarquer que le nombre de chiffres nécessaire pour écrire un entier a en base b est égal à la partie entière de logb(a).

Nombre de Fermat et primalité

La raison historique de l'étude des nombres de Fermat est la recherche de nombres premiers. Fermat connaissait déjà la proposition suivante :

  • Soit k un entier, le nombre 2k + 1 est un nombre premier seulement si k est une puissance de deux.

Pierre de Fermat a conjecturé que la réciproque était vraie, il a montré que :

F0 = 3 est premier
F1 = 5 est premier
F2 = 17 est premier
F3 = 257 est premier
et F4 = 65537 est premier

Actuellement, on ne connaît que cinq nombres de Fermat premiers, ceux cités ci-dessus.

On ignore encore s'il en existe d'autres, mais on sait que les nombres de Fermat Fn, pour n entre 5 et 32, sont tous composés ; F33 est le plus petit nombre de Fermat dont on ne sait pas s'il est premier ou composé.

Le plus grand nombre de Fermat dont on sait qu'il est composé est actuellement F2 478 782.


Démonstrations
  • Soit k un entier, le nombre 2k + 1 est un nombre premier seulement si k est une puissance de deux.

Si k n'est pas une puissance de deux, alors il existe deux entiers a et b tel que a est impair et différent de un et a.b = k. On dispose alors des égalités suivantes :

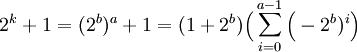
2^k + 1 = (2^b)^a + 1 = (1 + 2^b)\Big( \sum_{i=0}^{a-1} \Big (-2^b)^i \Big)

Ce qui montre que 2b + 1 divise 2k + 1 qui ne peut donc être premier.

Factorisation des nombres de Fermat composés

Euler utilise une méthode de Fermat pour démontrer que F5 n'est pas premier. Il démontre pour cela trois propositions :

  • Un facteur premier du nombre de Fermat Fn est de la forme k. 2 m + 1 où k est un entier impair, et m > = n + 2.
  • L'entier k de la proposition précédente possède un facteur premier impair.
  • F5 est divisible par 641.

Le cas général est un problème difficile du fait de la taille des entiers Fn, même pour des valeurs relativement faibles de n. Actuellement, le plus grand nombre de Fermat dont on connaisse la factorisation complète est F11 dont le plus grand des cinq diviseurs premiers a 560 chiffres (la factorisation complète de Fn, pour n entre 5 et 10, est, elle aussi, entièrement connue). En ce qui concerne F12, on sait qu'il est composé mais c'est le plus petit nombre de Fermat dont on ne connaisse pas la factorisation complète (on ne connaît pour l'instant que cinq des diviseurs premiers de F12). Quant à F14, c'est le plus petit nombre de Fermat composé dont on ne connaisse aucun diviseur premier.


Démonstrations
  • Un facteur premier p du nombre de Fermat Fn est de la forme k 2n+1 + 1 où k est un entier.

Fn est congru à zéro modulo p. On en déduit que 22n est congru à -1 modulo p et 22n+1 à 1 modulo p.

Montrons que l'ordre multiplicatif de 2 est 2n+1 dans l'anneau Z/pZ. Soit m l'ordre multiplicatif de 2, m est un diviseur de 2n+1, donc il existe un entier θ tel que m = 2θ. L'entier 22θ est congru à un modulo p donc si h est un entier strictement supérieur à θ, 22h est aussi congru à un modulo p, si θ est strictement plus petit que n + 1 alors 22n est congru à un modulo p ce qui est faux car nous avons montré qu'il est congru à -1.

De plus, le petit théorème de Fermat montre que 2p-1 est congru à un modulo p. Ce résultat et le fait que l'ordre multiplicatif de 2 est 2n+1 dans Z/pZ montre que p - 1 est un multiple de 2n+1. Ce qui termine la démonstration.

  • L'entier k de la proposition précédente possède un facteur premier impair.

Si k est une puissance de deux, alors p est un nombre premier de Fermat différent de Fn, or les nombres de Fermat n'ont pas de facteur commun. Cette remarque termine la démonstration.

  • F5 est divisible par 641.

Un diviseur premier de F5 est de la forme 64.k + 1. Les valeurs de k possibles sont 3, 5, 6, 7, 9, 10 ... Les valeurs 5 et 6 ne correspondent pas à des nombres premiers, les valeurs à tester sont donc 193, 449, 557 et 641. Euler limite donc l'étude à quatre cas au lieu de plus d'une centaine. Etudions le cas où k est égal à 10.

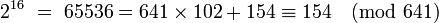
2^{16} \ = \ 65 536 = 641 \times 102 + 154 \equiv 154 \pmod {641}\,
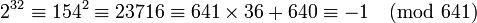
2^{32} \equiv 154^2 \equiv 23716 \equiv 641 \times 36 + 640 \equiv -1 \pmod {641} \,

Ce qui montre que 232 + 1 est congru à zéro modulo 641 et la proposition est démontrée.

Polygone régulier

Article détaillé : Polynôme cyclotomique.

Carl Friedrich Gauss a établi un lien entre ces nombres et la construction à la règle et au compas des polygones réguliers : un polygone régulier à n côtés peut être construit à la règle et au compas si et seulement si n est une puissance de 2, ou le produit d'une puissance de 2 et de nombres de Fermat premiers distincts.

Par exemple, le pentagone régulier est constructible à la règle et au compas puisque 5 est un nombre de Fermat premier ; de même, un polygone à 340 côtés est constructible à la règle et au compas puisque 340 = 22.F1.F2.

Généralisation

Il est possible de généraliser une partie des résultats obtenus pour les nombres de Fermat.

Pour que m = ab + 1 soit premier, a doit être pair (a = 2k) et b une puissance de 2 (b = 2n).

On appelle ces nombres les nombres de Fermat généralisés.

Notes et références

Notes

  1. ↑ Pierre de Fermat Lettre de Fermat à Frénicle du 18 octobre 1640 lire
  2. ↑ On cite aussi une lettre qu'on suppose être d'août 1640, où Fermat écrit : « Mais voici ce que j'admire le plus : c'est que je suis quasi persuadé que tous les nombres progressifs augmentés de l'unité, desquels les exposants sont des nombres de la progression double, sont nombres premiers, comme 3, 5, 17, 257, 65537, 4 294 967 297 et le suivant de 20 lettres 18 446 744 073 709 551 617 ; etc. Je n'en ai pas la démonstration exacte, mais j'ai exclu si grande quantité de diviseurs par démonstrations infaillibles, et j'ai de si grandes lumières, qui établissent ma pensée, que j'aurois peine à me dédire. » (Fermat, Lettre XLIII à Frénicle, août ? 1640, dans Œuvres de Fermat, t. 2, Paris, 1894, p. 206, en ligne.)
  3. ↑ Pierre de Fermat Correspondance Marin de Mersenne 25 Décembre 1640
  4. ↑ « Potestates omnes numeri 2, quarum exponentes sunt termini progressionis geometricæ ejusdem numeri 2, unitate auctae, sunt numeri primi » « Toutes les puissances du nombre 2 dont les exposants sont des termes de la progression géométrique du même nombre 2, donnent, si on les augmente d'une unité, des nombres premiers ».
  5. ↑ « propositiones aliquot quarum demonstrationem a nobis ignorari non diffitemur (...) Quaeritur demonstratio illius propositionis, pulchræ sane, sed et verissimæ » (« quelques propositions dont nous ne nierons pas ignorer la démonstration (...) Il reste à trouver une démonstration de cette proposition, certainement belle mais aussi très vraie » Œuvres de Fermat, Paris, t. 2, Paris, 1894, en ligne, lettre XCVI, pp. 402-405.
  6. ↑ Œuvres de Fermat, Paris, t. 2, Paris, 1894, en ligne, lettre CI, point 5, pp. 433-434.
  7. ↑ C'est l'interprétation que donne H.M. Edwards, Fermat's Last Theorem, Springer, 1977, p. 24, prenant position contre les vues contraires de E.T. Bell, The Last Problem, New York, 1961, p. 256.
  8. ↑ Leonhard Euler Observationes de theoremate quodam Fermatiano aliisque ad numeros primos spectantibus Commentarii academiae scientiarum Petropolitanae (6) 1738 p 102-103 1732
  9. ↑ Leonhard Euler Theoremata circa divisors numerorum Novi commentarii academiae scientiarum Petropolitanae (1) 1750 p 20 à 48 1747/48
  10. ↑ N. Lippi and J. Frey Biographies of Mathematicians-Marin Mersenne Université de St Andrew 1998
  11. ↑ L. Durman Histoire des nombres de Fermat sur Distributed search for Fermat number divisors 2003
  12. ↑ S. W. Golomb On the sum of the reciprocals of the Fermat numbers and related irrationalities Canad. J. Math. 15(1963), 475--478

Voir aussi

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre de Fermat ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article 4294967297 de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • 4294967297 (nombre) — Nombre de Fermat Pierre de Fermat étudie les propriétés des nombres portant maintenant son nom. Un nombre de Fermat est un entier naturel qui peut s écrire sous la forme 22n + 1, avec n entier. Le ne nombre de Fermat, 22n + 1, est noté Fn. Ces… …   Wikipédia en Français

  • Числа Ферма — числа вида , где n неотрицательное целое число. Последовательность чисел Ферма начинается так: 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, … (последовательность A000215 в OEIS) Содержание 1 История 2 …   Википедия

  • Число Ферма — Числа Ферма числа вида . Изучение чисел такого вида начал Ферма, который выдвинул гипотезу, что все они простые. Однако, эта гипотеза была опровергнута Эйлером в 1732 году, нашедшим разложение числа F5 на простые делители: Последовательность… …   Википедия

  • Простые числа Ферма — Числа Ферма числа вида . Изучение чисел такого вида начал Ферма, который выдвинул гипотезу, что все они простые. Однако, эта гипотеза была опровергнута Эйлером в 1732 году, нашедшим разложение числа F5 на простые делители: Последовательность… …   Википедия

  • Fermat number — In mathematics, a Fermat number, named after Pierre de Fermat who first studied them, is a positive integer of the form:F {n} = 2^{2^{ overset{n} {} + 1where n is a nonnegative integer. The first nine Fermat numbers are OEIS|id=A000215:As of|2008 …   Wikipedia

  • 600 (number) — For the year 600, see 600 BC or 600 AD. ← 599 601 → 600 List of numbers Integers ← …   Wikipedia

  • 1000000000 (number) — List of numbers – Integers 100000000 1000000000 10000000000 Cardinal One billion (short scale) One thousand million (long scale) Ordinal One billionth (short scale) Factorization 29 · 59 Binary 111011100110101100101000000000 He …   Wikipedia

  • Fermat'sche Primzahl — Eine Fermat Zahl, benannt nach dem französischen Mathematiker Pierre de Fermat, ist eine Zahl der Form wobei n eine natürliche Zahl ist. Die ersten Fermat Zahlen sind 3, 5, 17, 257, 65537, … (Folge A000215 in OEIS) Eine Fermat Zahl, die… …   Deutsch Wikipedia

  • Fermat-Zahl — Eine Fermat Zahl, benannt nach dem französischen Mathematiker Pierre de Fermat, ist eine Zahl der Form wobei n eine nichtnegative ganze Zahl ist. Die ersten Fermat Zahlen sind 3, 5, 17, 257, 65537, … (Folge A000215 in OEIS) Eine Fermat Zahl, die… …   Deutsch Wikipedia

  • Fermatsche Primzahl — Eine Fermat Zahl, benannt nach dem französischen Mathematiker Pierre de Fermat, ist eine Zahl der Form wobei n eine natürliche Zahl ist. Die ersten Fermat Zahlen sind 3, 5, 17, 257, 65537, … (Folge A000215 in OEIS) Eine Fermat Zahl, die… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”