- Nombre de Mersenne
-
Nombre premier de Mersenne
En mathématiques et plus précisément en arithmétique modulaire, un nombre premier de Mersenne est un nombre premier s'écrivant sous la forme 2p - 1, p étant premier. Ces nombres premiers doivent leur nom à un érudit et mathématicien français du XVIIe siècle, Marin Mersenne. Les nombres premiers de Mersenne sont, en base 2 (binaire), les répunits qui sont premiers.
Plus généralement, les nombres de Mersenne (pas nécessairement premiers, mais candidats à l'être) sont les nombres de la forme 2p - 1, avec p premier. On utilise la notation Mp = 2p - 1.
Les plus petits nombres premiers de Mersenne sont :
- 3 = 22-1
- 7 = 23-1
- 31 = 25-1
- 127 = 27-1
- Mais 2047 = 211-1 = 23 x 89 est un nombre de Mersenne, mais non premier.
On démontre qu'un entier de la forme 2n-1 ne peut pas être premier si n n'est pas lui-même premier. Ainsi 24-1=15 n'est pas de Mersenne, ni premier.
Sommaire
Propriétés des nombres de Mersenne
Les nombres de Mersenne ont les propriétés suivantes :
- Si n n'est pas premier (par exemple le produit n = rs où ni r, ni s n'est égal à 1) alors le nombre 2rs − 1 n'est pas premier.
En effet, en remarquant que la suite des r premiers termes de la suite géométrique
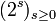 est égale à:
est égale à: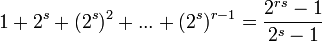 , on prouve que
, on prouve que 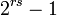 est divisible par
est divisible par 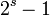 qui est différent de 1 dès que s est également distinct de 1.
qui est différent de 1 dès que s est également distinct de 1.Remarque : on peut également utiliser la formule
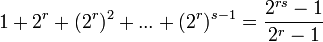 , pour prouver ce résultat.
, pour prouver ce résultat.Ainsi, lorsque l'on cherche des nombres premiers via les nombres de Mersenne, on sait déjà qu'il faut éviter les candidats comme
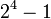 (i.e. 15),
(i.e. 15), 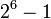 (i.e. 63) ou
(i.e. 63) ou 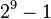 (i.e. 511 =
(i.e. 511 = 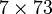 ).
).L'idée est maintenant d'affuter les critères de sélection des nombres premiers
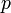 ...
...- Mn est la somme de coefficients binomiaux moins 1 :
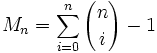 .
.
- Si a divise Mq (q premier) alors a possède les propriétés suivantes :
![a \equiv 1 [2q]](/pictures/frwiki/98/bce2394113961111f6a0ac2efac08f28.png) , et :
, et : ![a \equiv \pm 1 [8]](/pictures/frwiki/101/e215a0caf9fe3650edfc5872dbda3339.png) .
.
- Un théorème d'Euler entraîne que : Mq (q premier) est premier si et seulement s'il existe une unique paire (x,y) telle que : Mq = (2x)2 + 3(3y)2 avec q >= 5 . Très récemment, Bas Jansen a étudié Mq = x2 + dy2 pour d=0,48 .
- Soit q = 3 (mod 4) premier. 2q + 1 est aussi premier si et seulement si : 2q+1 divise Mq.
- Reix a récemment montré que les nombres de Mersenne Mq (q premier > 3), premiers ou non, s'écrivent : Mq = (8x)2 − (3qy)2 = (1 + Sq)2 − (Dq)2 . Évidemment, si la paire (x, y) est unique, alors Mq est premier.
- Ramanujan a montré que l'équation : Mq = 6 + x2 a seulement trois solutions où q est premier : 3, 5, et 7 (et deux solutions où q est non premier).
- Tous les facteurs premiers d'un nombre de Mersenne associé au nombre premier p sont de la forme kp+1 où k est un entier naturel. Deux nombres de Mersenne distincts sont toujours premiers entre eux.
Historique
Les nombres premiers de Mersenne sont liés aux nombres parfaits, qui sont les nombres égaux à la somme de leurs diviseurs propres. C'est cette connexion qui a motivé historiquement l'étude des nombres premiers de Mersenne. Dès le IVe siècle av. J.-C., Euclide démontrait que si M = 2p - 1 est un nombre premier, alors M(M+1)/2 = 2(p-1)(2p - 1) est un nombre parfait. Deux millénaires plus tard, au XVIIe siècle, Euler prouvait que tous les nombres parfaits pairs ont cette forme. Aucun nombre parfait impair n'est connu, une démonstration par l'absurde montre qu'il n'existe aucun nombre parfait impair.
Ma divise Mp si a divise p. Donc pour que Mp soit premier, il faut que p soit premier. Cela simplifie déjà la recherche de nombres premiers de Mersenne. La réciproque n'est pas vraie: Mp peut être composé alors que p est premier ; le plus petit exemple est 211-1 = 23×89.
Pour les nombres de Mersenne il existe une méthode (comparativement) très rapide pour déterminer s'ils sont premiers, développée à l'origine par Lucas en 1878 et améliorée par Derrick Lehmer dans les années 1930. On peut effectivement montrer que pour un nombre premier p impair Mp = 2p − 1 est premier si et seulement si Mp divise Sp − 1, où S1 = 4 et pour k > 1,
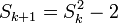 .
.Mersenne n'a pas inventé les nombres de Mersenne, mais il a fourni une liste de nombres premiers de Mersenne jusqu’à l'exposant 257. Malheureusement cette liste était fausse : elle incluait par erreur 67 et 257, et omettait 61, 89 et 107.
Les quatre premiers nombres premiers de Mersenne étaient connus dès l'Antiquité. Le cinquième (213-1) a été découvert avant 1461 par un inconnu. Les deux suivants ont été trouvés par Cataldi en 1588. Plus d'un siècle plus tard, en 1750, Euler en trouva encore un. Le suivant dans l'ordre chronologique (mais non numérique) a été trouvé par Lucas en 1876, puis un par Pervushin en 1883. Deux autres ont été trouvés au début du XXe siècle par Powers en 1911 et en 1914.
La recherche pour les nombres premiers de Mersenne fut révolutionnée par l'introduction des calculateurs électroniques. La première identification d'un nombre de Mersenne par ce moyen eut lieu à 22 heures le 30 janvier 1952 par un ordinateur SWAC à l'Institut d'Analyse Numérique (Institute for Numerical Analysis) du campus de Université de Californie - Los Angeles, sous la direction de Derrick Lehmer, avec un programme écrit par R.M. Robinson.
C'était le premier nombre premier de Mersenne identifié depuis 38 ans. Le suivant fut trouvé moins de deux heures plus tard par le même ordinateur, qui en trouva trois de plus dans les mois suivants.
En juin 2009, 47 nombres premiers de Mersenne étaient connus, le plus grand étant 243 112 609-1. Comme plusieurs de ses prédécesseurs, il a été découvert par un calcul distribué sous l'égide du projet GIMPS, Great Internet Mersenne Prime Search (qui signifie « grande recherche par Internet de nombres premiers de Mersenne »).
Liste
En juin 2009, 47 nombres premiers de Mersenne Mp=2p-1 étaient connus.
# p Mp Nombre
de chiffresDate
de découverteDécouvreur 1 2 3 1 Antiquité Inconnu 2 3 7 1 Antiquité Inconnu 3 5 31 2 Antiquité Inconnu 4 7 127 3 Antiquité Inconnu 5 13 8191 4 XIIIe siècle Ibn Fallus 6 17 131 071 6 1588 Cataldi 7 19 524 287 6 1588 Cataldi 8 31 2 147 483 647 10 1750 Euler 9 61 2 305 843 009 213 693 951 19 1883 Pervushin 10 89 618970019…449562111 27 1911 Powers 11 107 162259276…010288127 33 1914 Powers 12 127 170141183…884105727 39 1876 Lucas 13 521 686479766…115057151 157 30 janvier 1952 Robinson (Swac) 14 607 531137992…031728127 183 30 janvier 1952 Robinson (Swac) 15 1 279 104079321…168729087 386 25 juin 1952 Robinson (Swac) 16 2 203 147597991…697771007 664 7 octobre 1952 Robinson (Swac) 17 2 281 446087557…132836351 687 9 octobre 1952 Robinson (Swac) 18 3 217 259117086…909315071 969 8 septembre 1957 Riesel (Besk) 19 4 253 190797007…350484991 1 281 3 novembre 1961 Hurwitz (IBM) 20 4 423 285542542…608580607 1 332 3 novembre 1961 Hurwitz (IBM) 21 9 689 478220278…225754111 2 917 11 mai 1963 Gillies (Illiac) 22 9 941 346088282…789463551 2 993 16 mai 1963 Gillies (Illiac) 23 11 213 281411201…696392191 3 376 2 juin 1963 Gillies (Illiac) 24 19 937 431542479…968041471 6 002 4 mars 1971 Tuckerman (IBM) 25 21 701 448679166…511882751 6 533 30 octobre 1978 Noll & Glenn (CDC) 26 23 209 402874115…779264511 6 987 9 février 1979 Noll (CDC) 27 44 497 854509824…011228671 13 395 8 avril 1979 Nelson & Slowinski (Cray Research) 28 86 243 536927995…433438207 25 962 25 septembre 1982 Slowinski (Cray) 29 110 503 521928313…465515007 33 265 28 janvier 1988 Colquitt & Welsh (Nec) 30 132 049 512740276…730061311 39 751 19 septembre 1983 Slowinski (Cray) 31 216 091 746093103…815528447 65 050 1er septembre 1985 Slowinski (Cray) 32 756 839 174135906…544677887 227 832 19 février 1992 Slowinski & Gage 33 859 433 129498125…500142591 258 716 10 janvier 1994 Slowinski & Gage 34 1 257 787 412245773…089366527 378 632 3 septembre 1996 Slowinski & Gage 35 1 398 269 814717564…451315711 420 921 13 novembre 1996 GIMPS / Joel Armengaud 36 2 976 221 623340076…729201151 895 932 24 août 1997 GIMPS / Gordon Spence 37 3 021 377 127411683…024694271 909 526 27 janvier 1998 GIMPS / Roland Clarkson 38 6 972 593 437075744…924193791 2 098 960 1er juin 1999 GIMPS / Nayan Hajratwala 39 13 466 917 924947738…256259071 4 053 946 14 novembre 2001 GIMPS / Michael Cameron 40[N 1] 20 996 011 125976895…855682047 6 320 430 17 novembre 2003 GIMPS / Michael Shafer 41[N 1] 24 036 583 299410429…733969407 7 235 733 15 mai 2004 GIMPS / Josh Findley 42[N 1] 25 964 951 122164630…577077247 7 816 230 18 février 2005 GIMPS / Martin Nowak 43[N 1] 30 402 457 315416475…652943871 9 152 052 15 décembre 2005 GIMPS/ Cooper & Boone 44[N 1] 32 582 657 124575026…053967871 9 808 358 4 septembre 2006 GIMPS/ Cooper & Boone 45[N 1] 37 156 667 202254405…308220927 11 185 272 6 septembre 2008 GIMPS / Elvenich[1] 46[N 1] 42 643 801 169873516…562314751 12 837 064 12 avril 2009 GIMPS / Odd Magnar Strindmo 47[N 1] 43 112 609 316470267…697152511 12 978 189 23 août 2008 GIMPS / Smith[1] Note
- ↑ a , b , c , d , e , f , g et h On ne sait pas s'il existe ou non un ou plusieurs autres nombres premiers de Mersenne entre le 39e (M13 466 917) et le 47e (M43 112 609). Dans cet intervalle, le classement est donc provisoire. Déjà le 29e nombre premier de Mersenne fut découvert après le 30e et le 31e, de même que M43 112 609 fut découvert quinze jours avant M37 156 667, plus petit. De même le 46e (M42 643 801) a été découvert neuf mois après le 47e M43 112 609).
Voir aussi
Liens internes
Liens externes
- ↑ a et b (en) Page d'accueil du GIMPS, Découverte des 45e et 46e nombres premiers de Mersenne
- (en) http://www.utm.edu/research/primes/mersenne.shtml
- (en) Découverte du 42e
- (en) Mq = (8x)2 - (3qy)2 Preuve
- (en) Nombres de Mersenne
- (en) Nombres de Mersenne premiers
- (en) Mq = x2 + d.y2 Thèse
- Portail des mathématiques
Catégories : Arithmétique modulaire | Nombre premier | Nombre premier de Mersenne
Wikimedia Foundation. 2010.

