- Graphe tesseract
-
Graphe tesseract 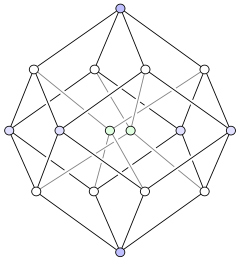
Une représentation du graphe tesseract.Nombre de sommets 16 Nombre d'arêtes 32 Distribution des degrés 4-régulier Rayon 4 Diamètre 4 Maille 4 Automorphismes 384 Nombre chromatique 2 Indice chromatique 4 Propriétés Arête-transitif
Biparti
Distance-régulier
Hamiltonien
Parfait
Régulier
Sommet-transitif
Intégral
Graphe de Cayley
Distance-unitémodifier 
Le graphe tesseract est, en théorie des graphes, un graphe 4-régulier possédant 16 sommets et 32 arêtes.
Sommaire
Construction
Une façon de construire le graphe tesseract est de le considérer comme le squelette de l'hypercube en dimension 4, un solide appelé tesseract. On peut alors le définir comme le produit cartésien[1] de 4 graphes complets K2, soit :

Il peut être également obtenu par produit cartésien du graphe hexaédrique et du graphe complet K2, soit :

Propriétés
Propriétés générales
Le diamètre du graphe tesseract, l'excentricité maximale de ses sommets, est 4, son rayon, l'excentricité minimale de ses sommets, est 4 et sa maille, la longueur de son plus court cycle, est 4. Il s'agit d'un graphe 4-sommet-connexe et d'un graphe 4-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 4 sommets ou de 4 arêtes.
Coloriage
Le nombre chromatique du graphe tesseract est 2. C'est-à-dire qu'il est possible de le colorer avec 2 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du graphe tesseract est 4. Il existe donc une 4-coloration des arêtes du graphe tels que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Il est possible de compter les colorations distinctes d'un graphe. Cela donne une fonction dépendant du nombre de couleurs autorisé. Cette fonction est polynomiale et est qualifiée de polynôme chromatique du graphe. Ce polynôme admet pour racines tous les entiers positifs ou nuls strictement inférieurs à 2 et est de degrés 16. Il est égal à : (x − 1)x(x14 − 31x13 + 465x12 − 4471x11 + 30793x10 − 160807x9 + 657229x8 − 2137667x7 + 5564285x6 − 11536667x5 + 18740317x4 − 23081607x3 + 20308039x2 − 11372201x + 3040575).
Propriétés algébriques
Le graphe tesseract est symétrique, c'est-à-dire que son groupe d'automorphismes agit transitivement sur ses arêtes, ses sommets et ses arcs. Il est donc également arête-transitif et sommet-transitif. C'est l'unique graphe symétrique régulier de degrés 4 à 16 sommets[2].
Le groupe d'automorphisme Γ(Q4) du graphe tesseract est d'ordre 384 et est isomorphe au produit en couronne des groupes symétriques S2 et S4 :
 [3]. Le produit en couronne de A et B étant défini comme le produit semi-direct
[3]. Le produit en couronne de A et B étant défini comme le produit semi-direct  où AB est l'ensemble des fonctions de A dans B et où A agit sur AB par décalage d'indice :
où AB est l'ensemble des fonctions de A dans B et où A agit sur AB par décalage d'indice :(g.λ)(s) = λ(g − 1s) pour  et
et  .
.L'hypercube Q4 est un graphe de Cayley Cay(G, S) avec :

S = {(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)} Cela découle d'une propriété plus générale statuant que tous les graphes de Hamming sont des graphes de Cayley[4].
Le polynôme caractéristique du graphe tesseract est : (x − 4)(x − 2)4x6(x + 2)4(x + 4). Un autre graphe possède le même polynôme caractéristique, et donc le même spectre : le graphe de Hoffman. Le graphe tesseract et le graphe de Hoffman sont donc cospectraux. Par ailleurs ce polynôme caractéristique n'admet que des racines entières. Le graphe tesseract est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers.
Voir aussi
Liens internes
Liens externes
Références
- (fr) J-C. Bermond, P. Fraigniaud, A. Germa, M-C. Heydemann, E. Lazard, P. Michallon, A. Raspaud, D. Sotteau, M. Syska et D. Trystram - Communications dans les réseaux de processeurs, Masson, 1994, (ISBN 2225844100). Paru sous le pseudonyme Jean de Rumeur.
- (en) Neil J.A. Sloane, The On-Line Encyclopedia of Integer Sequences, A087101 on-line
- (en) F. Harary - The Automorphism Group of a Hypercube, Journal of Universal Computer Science, volume 6, pages 136-138, 2000.
- (en) Cai Heng Li - Cayley graph in Encyclopaedia of Mathematics, Springer, (ISBN 1402006098). on-line
Wikimedia Foundation. 2010.
