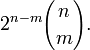Tesséract

Un hypercube est, en géométrie, un analogue n-dimensionnel d'un carré (n = 2) et d'un cube (n = 3). C'est une figure fermée, compacte, convexe constituée de groupes de segments parallèles opposés alignés dans chacune des dimensions de l'espace, en angle droit les uns les autres.

Un hypercube n-dimensionnel est aussi appelé un n-cube. Le terme « polytope de mesure » (qui est apparemment dû à Coxeter ; voir Coxeter 1973) est aussi utilisé mais il est rare.

Sommaire 1 Définition 2 Représenter un hypercube de dimension n 3 4 dimensions 4 n dimensions 5 Éléments 6 Rotation d'un n-cube 7 Représentations artistiques 8 Notes et références 9 Voir aussi 9.1 Articles connexes 9.2 Bibliographie 9.3 Liens externes

Définition

Si E est un espace euclidien de dimension n muni d'une base orthonormale, on définit un hypercube unité comme l'hypervolume délimité par les 2ⁿ points dans E ayant des coordonnées égales à 0 ou 1 reliés par des segments de droite. Les hypercubes sont les figures obtenues à partir de l'hypercube unité par des similitudes.

Représenter un hypercube de dimension n

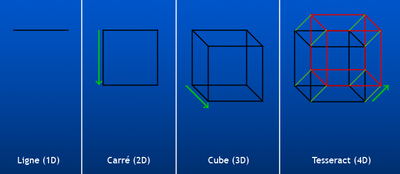
Pour représenter un hypercube de dimension n, on procède comme suit :

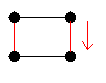
• Dimension 1 : Un point est un hypercube de dimension zéro. Si on déplace ce point d'une longueur unité, il balaiera un segment de droite, qui est un hypercube unité de dimension un

• Dimension 2 : Si on déplace ce segment d'une longueur unité dans une direction perpendiculaire à partir de lui-même ; il balaie un carré bi-dimensionnel.

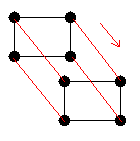
• Dimension 3 : Si on déplace le carré d'une longueur unité dans la direction perpendiculaire à l'emplacement de celui-ci, il engendrera un cube tri-dimensionnel.

• Dimension 4 : Si on déplace le cube d'une longueur unité dans la quatrième dimension, il engendrera un hypercube unité quadri-dimensionnel (un tesseract unité).

…

• Dimension n > 3 : On trace un hypercube de dimension n-1, on reproduit son image et on lie les points deux à deux.

En résumé, la construction d'un hypercube se fait par la translation du cube de dimension inférieure selon un axe perpendiculaire aux dimensions de ce cube.

Les hypercubes sont une des quelques familles de polytopes réguliers qui sont représentés dans un nombre quelconque de dimensions. Le polytope dual d'un hypercube est appelé un polytope croisé. le 1-squelette d'un hypercube est un graphe hypercube.

Une généralisation du cube aux dimensions plus grandes que trois est appelée un « hypercube », « n-cube » ou « polytope mesure ». Le tesseract est l'hypercube quadri-dimensionnel ou 4-cube. C'est un polytope régulier. C'est aussi un cas particulier de parallélotope : un hypercube est un parallélotope droit dont les arêtes sont de même longueur.

4 dimensions

L’hypercube à quatre dimensions est également appelé tesseract en anglais, d'après Charles Howard Hinton.

D'après la formule de Gardner, on peut retrouver les propriétés du tesseract en développant (2x + 1)⁴ :

(2x + 1)⁴ = 16x⁴ + 32x³ + 24x² + 8x + 1

Donc l'hypercube est composé de :

• 16 sommets ;
• 32 arêtes ;
• 8 faces cubiques (soit 24 faces planes) : chacune des faces du tesseract est un cube.

L'intersection d'un hypercube avec un hyperplan donne l'équation cartésienne :

ax + by + cz + dw = e

Avec les quatre coordonnées de l'hyperespace de dimension 4, à savoir x, y, z, et w. En réalité, un hyperplan en quatre dimensions peut être comparé à l'espace tridimensionnel, c’est-à-dire que l'intersection d'un hypercube avec un plan est en fait une projection 3D de cet hypercube.

• "Volume" (quadridimentionnel) : c⁴
• "Surface externe" (tridimentionnelle) : 8c³
• "Aire totale" (bidimentionnelle) : 24c²

(avec c le côté de l'hypercube)

Les faces d'un hypercube sont :

• Avant / Arrière
• Gauche / Droite
• Haut / Bas
• Ana / Kata

n dimensions

Un hypercube à n dimensions possède :

• V_n = 2ⁿ sommets ;
• S_n = 2 × S_n-1 + V_n-1 arêtes ; (ou n × 2^n-1)
• F_n = 2 × F_n-1 + S_n-1 faces planes ;
• HF_n = 2 × HF_n-1 + F_n-1 hyperfaces (cubes ou faces cubiques) ;
• Il en va de même pour les hyperfaces en 5 dimensions (faces hypercubiques) etc.
• De manière générale, le nombre de faces à k dimensions d'un hypercube à n dimension est égal à

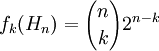
• Le nombre total de faces d'un hypercube est de 3ⁿ − 1
• Volume = cⁿ avec c le côté de l'hypercube.

Si on le coupe en n tranches par des hyperplans perpendiculaires à la diagonale, les volumes des tranches sont les nombres d'Euler.

• Aire totale = F_nc² avec F_n le nombre de faces
• Un polytope dual : l'hyperoctaèdre à n dimensions également (appelé aussi n-polytope croisé)

Éléments

Un hypercube de dimension n possède 2n cotés (un segment 1-dimensionnel a deux points aux extrémités ; un carré 2-dimensionnel a quatre bords ; un cube 3-dimensionnel a 6 faces 2-dimensionnelles ; un hypercube 4-dimensionnel (tesseract) a 8 cellules). Le nombre de sommets (points) d'un hypercube est 2ⁿ (un cube a 2³ sommets, par exemple).

Le nombre d'hypercubes m-dimensionnels (comme désigné sous le nom m-cube ci-dessus) sur la frontière d'un n-cube est :

Par exemple, la frontière d'un 4-cube contient 8 cubes, 24 carrés, 32 segments et 16 sommets.

Éléments d'hypercube

n-cube	Graphe	Noms Symbole de Schläfli Coxeter-Dynkin	Sommets (0-faces)	Arêtes (1-faces)	Faces (2-faces)	Cellules (3-faces)	(4-faces)	(5-faces)	(6-faces)	(7-faces)	(8-faces)
0-cube		Point -	1
1-cube		Digone {} ou {2}	2	1
2-cube		Carré Tétragone {4}	4	4	1
3-cube	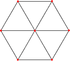	Cube Hexaèdre {4,3}	8	12	6	1
4-cube		Tesseract octachore {4,3,3}	16	32	24	8	1
5-cube		Penteract déca-5-tope {4,3,3,3}	32	80	80	40	10	1
6-cube		Hexeract dodéca-6-tope {4,3,3,3,3}	64	192	240	160	60	12	1
7-cube		Hepteract tétradéca-7-tope {4,3,3,3,3,3}	128	448	672	560	280	84	14	1
8-cube		Octeract hexadéca-8-tope {4,3,3,3,3,3,3}	256	1024	1792	1792	1120	448	112	16	1
9-cube		Ennéneract octadéca-9-tope {4,3,3,3,3,3,3,3}	512	2304	4608	5376	4032	2016	672	144	18

Rotation d'un n-cube

La définition des rotations dans un espace euclidien quelconque passe par l'algèbre linéaire, et leurs propriétés ne se déduisent pas aisément de celles des rotations en dimension 3. On montre cependant que, de même qu'il est possible de faire tourner un cube autour d'une arête, on peut faire tourner un tesseract autour d'une de ses 2-faces carrées^[1], qu'un hypercube 5-dimensionnel peut tourner autour d'un cube entier, etc.

Représentations artistiques

• Dans le film de science-fiction Cube² : Hypercube, les héros sont enfermés dans un tesseract, ou du moins ils évoluent en se déplaçant d'un cube à l'autre parmi les faces de l'hypercube. D'un cube à l'autre, l'orientation de la pesanteur peut varier (en tout cas les personnages le ressentent quand ils passent d'un cube à l'autre) le temps peut se dilater ou se contracter, et les personnages sont amenés à rencontrer des doubles d'eux-mêmes à cause de la superposition de futurs possibles. Mais le lien entre ces propriétés et le fait que l'histoire se déroule dans un tesseract n'est pas explicite.

• En architecture, l'Arche de la Défense à Paris en France, est une projection en trois dimensions d'un hypercube.

• La peinture Crucifixion (Corpus Hypercubus), par Salvador Dalí, 1954, décrit un Jésus crucifié sur le patron d'un hypercube. Il est exposé au Metropolitan Museum of Art à New York.

Notes et références

Voir aussi

Articles connexes

• Tesseract
• Hypercube magique
• Tesseract magique
• Hypercube OLAP en informatique décisionnelle
• L'Arche de la Défense peut être considéré comme une représentation partielle d'un hypercube

Bibliographie

• Bowen, J. P., Hypercubes, Practical Computing, 5(4):97–99, avril 1982.
• Coxeter, H. S. M., Regular Polytopes. 3^e édition, Dover, 1973, p. 123. (ISBN 0-486-61480-8). p. 296,

Liens externes

• (en) Ken Perlin : comment visualiser un hypercube, par Ken Perlin.
• (fr) 4dimensions : Explication en français de la notion d'un espace à quatre dimensions par l'hypercube. Créé par Mounier Florian

• Portail de la géométrie