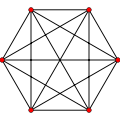
Graphe sommet-connexe
- Graphe sommet-connexe
-
En théorie des graphes, un graphe k-sommet-connexe (ou graphe k-connexe) est un graphe connexe qu'il est possible de déconnecter en supprimant k sommets et tel que ce k soit minimal. Il existe donc un ou plusieurs ensembles de k sommets dont la suppression rende le graphe déconnecté, mais la suppression de k-1 sommets, quels qu'ils soient, le fait demeurer connexe. Par convention, le graphe complet à k sommets est k-1 connexe.
Un graphe régulier de degré k est au plus k-sommet-connexe et k-arête-connexe. S'il est effectivement k-sommet-connexe et k-arête-connexe, il est qualifié de graphe optimalement connecté.
Exemples
- Pour tout n, le graphe complet Kn est optimalement connecté. Il est (n-1)-sommet-connexe, (n-1)-arête-connexe et (n-1)-régulier.
- Pour tout k>2 et tout l>1, le graphe moulin Wd(k,l) est 1-sommet-connexe. Pour le séparer en l composantes connexes, il suffit de supprimer son sommet de plus haut degré : son centre.
- Le graphe cycle Cn est 2-sommet-connexe pour tout n>3.
-
Le graphe de Biggs-Smith est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté.
-
Le graphe moulin Wd(5,4) devient déconnecté si on supprime son sommet central. Il est 1-sommet-connexe.
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Graphe sommet-connexe de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Graphe arête-connexe — En théorie des graphes, un graphe k arête connexe est un graphe connexe qu il est possible de déconnecter en supprimant k arêtes et tel que ce k soit minimal. Il existe donc un ou plusieurs ensembles de k arêtes dont la suppression rende le… … Wikipédia en Français
Graphe connexe — Sommaire 1 Définition 2 Propriétés 3 Algorithmes 4 Exemples 5 Voir aussi … Wikipédia en Français
Graphe de Petersen — Schéma classique du graphe de Petersen, sous la forme d un pentagone et d un pentagramme concentriques, reliés par cinq rayons. Nombre de sommets 10 Nombre d arêtes 15 Distribution des degrés 3 régulier … Wikipédia en Français
Graphe de Coxeter — Représentation du graphe de Coxeter. Nombre de sommets 28 Nombre d arêtes 42 Distribution des degrés 3 régulier Rayon 4 … Wikipédia en Français
Graphe croix — Représentation du graphe croix. Nombre de sommets 6 Nombre d arêtes 5 Distribution des degrés 1 (4 sommets) 2 (1 sommet) 4 (1 sommet) Rayon 2 … Wikipédia en Français
Graphe de Horton — Représentation du graphe de Horton. Nombre de sommets 96 Nombre d arêtes 144 Distribution des degrés 3 régulier Rayon 10 … Wikipédia en Français
Graphe de Nauru — Représentation du graphe de Nauru. Notation F24A Nombre de sommets 24 Nombre d arêtes 36 Distribution des degrés 3 régulier … Wikipédia en Français
Graphe antenne — Représentation du graphe antenne. Nombre de sommets 6 Nombre d arêtes 7 Distribution des degrés 1 (1 sommet) 2 (2 sommets) 3 (3 sommets) Rayon 2 … Wikipédia en Français
Graphe fléchette — Représentation du graphe fléchette. Nombre de sommets 5 Nombre d arêtes 6 Distribution des degrés 1 (1 sommet) 2 (2 sommets) 3 (1 sommet) 4 (1 sommet) Rayon … Wikipédia en Français
Graphe mite — Représentation du graphe mite. Nombre de sommets 6 Nombre d arêtes 7 Distribution des degrés 1 (2 sommets) 2 (2 sommets) 3 (1 sommet) 5 (1 sommet) Rayon 1 … Wikipédia en Français