- Graphe Hamiltonien
-
Graphe hamiltonien
En théorie des graphes, un graphe hamiltonien est un graphe possédant au moins un cycle passant par tous les sommets une et une seule fois. Un tel cycle élémentaire est alors appelé cycle hamiltonien. Un graphe hamiltonien ne doit pas être confondu avec un graphe eulérien.
Le plus petit graphe hamiltonien à n sommets est le graphe cycle Cn. Mais un graphe hamiltonien peut contenir plusieurs cycles hamiltoniens. Ainsi le graphe de Chvátal a 12 sommets, 24 arêtes et 370 cycles hamiltoniens distincts[1].
Trouver un cycle hamiltonien pour un graphe donné est un problème difficile sur le plan algorithmique, c'est-à-dire de type NP-complet. Le problème du voyageur de commerce s'apparente d'ailleurs à la recherche d'un cycle hamiltonien en ajoutant une contrainte : la minimalisation de son poids dans un graphe complet dont les arêtes sont pondérées.
Sommaire
Chemin hamiltonien
Les chemins hamiltoniens sont dus à William Rowan Hamilton qui était astronome royal en Irlande, au milieu du XIXe siècle. Dans un graphe, on qualifie d’hamiltonien un chemin qui passe une et une seule fois par chaque sommet du graphe. Un graphe possédant un cycle hamiltonien possède nécessairement un chemin hamiltonien, obtenu en enlevant une arête quelconque du cycle, mais la réciproque est fausse. Le problème du chemin Hamiltonien est aussi difficile que celui du cycle hamiltonien, puisqu'ils sont tous les deux NP-complets.
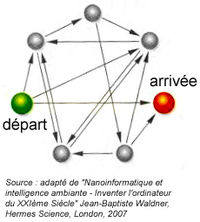Un chemin hamiltonien dans un graphe est un chemin qui passe par tous les sommets une fois et une seule[2].
Recherche d'un chemin hamiltonien par ordinateur à ADN
D'après les recherches de Leonard Adleman, ce problème pourrait être soluble efficacement (au moins en pratique) par un ordinateur à ADN. Il serait alors suffisamment complexe et significatif pour constituer une preuve indubitable de l’intérêt de ces nouvelles machines. L'idée est de représenter les arêtes du graphes par des séquences d'ADN qui peuvent s'assembler linéairement quand elles ont une extrêmité commune. Un polymère formé par ces séquences correspond donc à un chemin.
L'algorithme proposé par Adleman est le suivant:
- Générer un grand nombre de séquences, correspondant à des chemins aléatoires
- Filtrer (par exemple par la masse) pour ne garder que les chemins avec n sommets (où n est la taille du graphe)
- Filtrer pour ne garder que les chemins qui contiennent une fois chaque sommet
- S'il reste des séquences qui passent les deux filtres, le graphe a un chemin hamiltonien.
Bibliographie
- (en) Leonard Adleman, "An Abstract Theory of Computer Viruses", Springer-Verlag New York, Inc., 1990, ISBN 0-387-97196-3
- (en) Leonard Adleman, "Towards a (MATH)ematical theory of self-assembly. Technical Report 00-722", Department of Computer Science, University of Southern California, 2000, ISBN 2-7011-4032-3
- (fr) Jean-Baptiste Waldner, "Nano-informatique et intelligence ambiante - Inventer l'ordinateur du XXIe siècle", Hermes Science, London, 2006, ISBN 2-7462-1516-0
Références
- ↑ (en) Weisstein, Eric W [ttp://mathworld.wolfram.com/ChvatalGraph.html "Chvátal Graph" From MathWorld--A Wolfram Web Resource]
- ↑ Adapté de Nanoinformatique et intelligence ambiante - Inventer l'ordinateur du XXIe siècle Jean-Baptiste Waldner, Hermès Science, London, 2007 (avec la permission de l'auteur)
Liens externes
Portail des mathématiques
Portail de l’informatique
Catégories : Concept en théorie des graphes | Famille de graphes
Wikimedia Foundation. 2010.
