- Graphe de Moser
-
Graphe de Moser 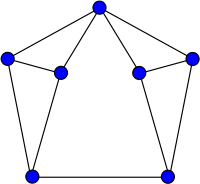
Représentation du graphe de Moser.Nombre de sommets 7 Nombre d'arêtes 11 Distribution des degrés 3 (6 sommets)
4 (1 sommet)Rayon 2 Diamètre 2 Maille 3 Automorphismes 8 Nombre chromatique 4 Indice chromatique 4 Propriétés Hamiltonien
Planaire
Distance-unitémodifier 
Le graphe de Moser est, en théorie des graphes, un graphe possédant 7 sommets et 11 arêtes.
Sommaire
Propriétés
Propriétés générales
Le diamètre du graphe de Moser, l'excentricité maximale de ses sommets, est 2, son rayon, l'excentricité minimale de ses sommets, est 2 et sa maille, la longueur de son plus court cycle, est 3. Il s'agit d'un graphe 2-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 2 sommets ou de 3 arêtes.
Il est possible de tracer le graphe de Moser sur un plan sans qu'aucune de ses arêtes se croisent. Le graphe de Moser est donc planaire. C'est également un graphe distance-unité : il peut s'obtenant à partir d'une collection de points du plan euclidien en reliant par une arête toutes les paires de points étant à une distance de 1.
Coloriage
Le nombre chromatique du graphe de Moser est 4. C'est-à-dire qu'il est possible de le colorer avec 4 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
Le problème de Hadwiger–Nelson, introduit en 1944 par Hugo Hadwiger et Edward Nelson, concerne le nombre minimal de couleur qu'il faut pour colorier le plan de façons à ce que deux points à une distance de 1 ne soient jamais de la même couleur[1]. Il peut être formalisé en théorie des graphes de la façon suivante : quel est le nombre chromatique maximal d'un graphe distance-unité ? Le problème est toujours ouvert mais le graphe de Golomb, avec son nombre chromatique égal à 4, fournit une borne inférieure, la meilleure connue à ce jour[2]. Un autre exemple connu, plus petit mais avec le même nombre chromatique, est le graphe de Moser[3].
L'indice chromatique du graphe de Moser est 4. Il existe donc une 4-coloration des arêtes du graphe tels que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Il est possible de compter les colorations distinctes du graphe de Moser. Cela donne une fonction dépendant du nombre de couleurs autorisé. C'est une fonction polynomiale et le polynôme qui lui est associé est qualifiée de polynôme chromatique. Ce polynôme de degré 7 admet pour racines tous les entiers positifs ou nuls strictement inférieurs à 4. Il est égal à : (x − 3)(x − 2)2(x − 1)x(x2 − 3x + 4).
Propriétés algébriques
Le groupe d'automorphismes du graphe de Moser est un groupe d'ordre 8.
Le polynôme caractéristique du graphe de Moser est : − (x + 1)2(x2 − 3)(x3 − 2x2 − 5x + 4). Le graphe de Moser est déterminé de façon unique par son spectre de graphe, l'ensemble des valeurs propres de sa matrice d'adjacence.
Voir aussi
Liens internes
Liens externes
- (en) Eric W. Weisstein, Moser Spindle (MathWorld)
Références
- O'Rourke, Joseph, « Problem 57: Chromatic Number of the Plane » sur The Open Problems Project.
- Soifer, A. The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of Its Creators New York: Springer, pp. 19-20, 2008.
- Moser, L. and Moser, W. "Problem 10." Canad. Math. Bull. 4, 187-189, 1961.
Wikimedia Foundation. 2010.
