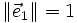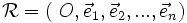Base orthonormée directe

Base orthonormée directe

Base orthonormale

Page d'aide sur l'homonymie Pour les articles homonymes, voir BON.

Une base orthonormale (BON) est une structure mathématique.

Sommaire

Définition

Soit En un espace vectoriel euclidien de dimension n, où n est un entier naturel non nul, et 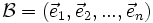\mathcal B = ( \vec e_1 , \vec e_2 , ... , \vec e_n), une base de En.

  • Si n = 1, alors 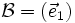\mathcal B = ( \vec e_1) est dite orthonormale si et seulement si
\| \vec e_1 \| = 1
  • Si n > 1, alors 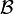\mathcal B est orthonormale si et seulement si
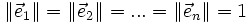
\| \vec e_1 \| = \| \vec e_2 \| = ... = \| \vec e_n \| = 1
et,
pour tout 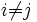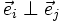i \not = j, \vec e_i \perp \vec e_j ( c'est-à-dire 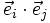\vec e_i \cdot \vec e_j = 0 )

Une base orthonormale est donc une base où tous les vecteurs de la base sont de norme 1 et sont orthogonaux 2 à 2. Cette définition s'applique aussi sur un espace hermitien. Il correspond à une généralisation aux complexes d'un espace euclidien.

Repère orthonormal (ou orthonormé)

Soient An un espace affine euclidien associé à l'espace vectoriel euclidien En et O un point quelconque de An, alors le repère

\mathcal R = (\ O , \vec e_1 , \vec e_2 , ... , \vec e_n)

est dit orthonormal si et seulement si sa base associée 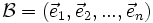\mathcal B = ( \vec e_1 , \vec e_2 , ... , \vec e_n) est elle-même orthonormale.

En géométrie dans l'espace

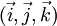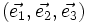En géométrie dans l'espace, la base est en général notée (\vec{i},\vec{j},\vec{k}) au lieu de (\vec{e_1},\vec{e_2},\vec{e_3}).

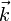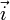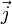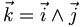La base est dite « directe » si \vec{k} est le produit vectoriel de \vec{i} et de \vec{j} (\vec{k} = \vec{i} \wedge \vec{j}).

Le terme « base orthonormale directe » est parfois abrégé par le sigle BOD.

Si la base associée à un repère est orthonormale directe, le repère est un repère orthonormal direct, terme parfois abrégé par le sigle ROND.

Voir l'article Orientation (mathématiques).


Orthonormalisation

Article détaillé : Procédé de Gram-Schmidt.

On peut à partir d'une base qui n'est pas orthonormale construire une base orthonormale. La méthode la plus répandue est l'orthogonalisation de Gram-Schmidt. Cette méthode permet de construire une base orthonormale à partir de toute base de l'espace.

Voir aussi

Articles de mathématiques en rapport avec l'algèbre bilinéaire
modifier


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Base orthonormale ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Base orthonormée directe de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Base orthonormée — Base orthonormale Pour les articles homonymes, voir BON. Une base orthonormale (BON) est une structure mathématique. Sommaire 1 Définition 2 Repère orthonormal (ou orthonormé) …   Wikipédia en Français

  • Base réciproque — Espace réciproque En physique, on utilise souvent des espaces abstraits pour caractériser les phénomènes, ce sont des espaces des phases. Dans le cas des ondes, l espace des phases est l espace des vecteurs d onde. Une onde plane et… …   Wikipédia en Français

  • Base (Algèbre Linéaire) — Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse être exprimé de manière… …   Wikipédia en Français

  • Base (algebre lineaire) — Base (algèbre linéaire) Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse… …   Wikipédia en Français

  • Base d'un espace — Base (algèbre linéaire) Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse… …   Wikipédia en Français

  • Base vectorielle — Base (algèbre linéaire) Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse… …   Wikipédia en Français

  • Base Canonique — Dans un espace vectoriel, une base canonique est une base qui se présente de manière naturelle d après la manière dont l espace vectoriel est présenté. C est ainsi que l on parle de la base canonique de , de la base canonique de l espace… …   Wikipédia en Français

  • Base (algèbre linéaire) — Pour les articles homonymes, voir Base. En mathématiques, et plus particulièrement en algèbre linéaire, une base d un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l espace puisse être exprimé de manière… …   Wikipédia en Français

  • Base orthonormale — Pour les articles homonymes, voir BON. En géométrie vectorielle, une base orthonormale, ou base orthonormée, (BON) d un espace euclidien ou hermitien est une base de cet espace vectoriel constituée de vecteurs de norme 1 et orthogonaux deux à… …   Wikipédia en Français

  • Base canonique — Dans un espace vectoriel, une base canonique est une base qui se présente de manière naturelle d après la manière dont l espace vectoriel est présenté. C est ainsi que l on parle de la base canonique de , de la base canonique de l espace… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”