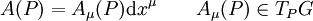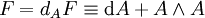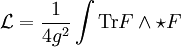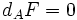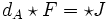- Équations de Yang-Mills
-
Équations de Yang-Mills
Une théorie de Yang-Mills est un type de théorie de jauge non abélienne, dont le premier exemple a été introduit dans les années 1950 par les physiciens Chen Ning Yang, et Robert Mills pour obtenir une description cohérente de l'interaction faible au sein des noyaux atomiques. Depuis, il a été réalisé que ce type de théorie, une fois incorporé dans le cadre de la théorie quantique des champs, permet une description de l'ensemble des interactions fondamentales de la physique des particules et est à la base conceptuelle du modèle standard[1].
Son expression mathématique moderne fait appel aux outils de la géométrie différentielle et des espaces fibrés. Bien que la formulation et le cadre géométrique de la théorie de Yang-Mills classique soient bien connus depuis longtemps, deux propriétés fondamentales n'ont toujours pas été démontrées mathématiquement :
- d'une part l’existence d'une théorie quantique des champs cohérente, fondée sur une théorie de Yang-Mills[2] ;
- d'autre part l'existence d'un gap de masse qui ne permet l'observation les gluons, particules élémentaires de la théorie quantique associés à toute théorie de Yang-Mills, que sous forme de combinaisons massives appelées boule de glue (glueball en anglais). Ce problème non résolu est intimement lié à celui du confinement de couleur qui affirme que seuls sont observables les états quantiques de charge nulle.
La résolution de ces deux points constitue l'un des problèmes du prix du millénaire[3].
En dehors de ces aspects associés à la physique quantique, la théorie de Yang-Mills classique est hautement non linéaire et les équations de Yang-Mills qui lui sont associées sont très difficiles à résoudre de façon exacte en dehors de cas particuliers. C'est cette non-linéarité, associée à une structure géométrique riche, qui donne aux théories de Yang-Mills toute leur complexité et en fait un sujet de recherche actif à la fois en mathématiques et en physique théorique.
Sommaire
Formulation technique et lagrangien de Yang-Mills
Pour définir une théorie de Yang-Mills il faut commencer par se donner un groupe de jauge G qui est un groupe de Lie et représente physiquement le groupe de symétrie locale de la théorie. L'invariance locale signifie que les équations de Yang-Mills seront inchangées sous l'action de transformations de G sur les champs physiques en chaque point de l'espace-temps.
Pour décrire la théorie, le meilleur point de vue est alors d'incorporer l'espace-temps et le groupe G au sein d'une même entité géométrique appelée espace fibré en G. On peut visualiser cet espace fibré par la donnée d'une copie du groupe G au-dessus de chaque point de l'espace-temps[4].
Une fois cet espace construit l'outil fondamental de l'analyse est la donnée d'une connexion A qui est un objet analogue au potentiel vecteur de la théorie éléctromagnétique. D'un point de vue mathématique une connexion est ce qui permet de définir un transport parallèle sur l'espace-fibré[5]. D'un point de vue de physique quantique, et pour prendre l'exemple plus simple de l'électromagnétisme, la connexion est ce qui permet de connaitre l'évolution de la phase d'une particule chargée, comme un électron en mouvement par exemple.
Pour définir complètement cette connexion, on peut la voir comme une forme différentielle sur l'espace-temps à valeur dans l'espace tangent du groupe de Lie G, ce qu'on appelle l'algèbre de Lie
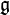de G. En tout point P de l'espace-temps elle peut s'écrireoù xμ sont des coordonnées sur l'espace-temps.
En première approche on peut aussi visualiser Aμ comme la donnée d'une matrice (dans la représentation adjointe de G) en chaque point de l'espace-temps.
On peut alors introduire le lagrangien de Yang-Mills, duquel découlent de nombreuses équations. Il est formulé en termes de la courbure F de la connexion A qui est exprimée par
et s'écrit
où Tr est la trace dans la représentation adjointe l'algèbre de Lie de
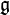. g est le seul paramètre libre de la théorie et correspond à la constante de couplage de la théorie de Yang-Mills.L'utilisation de ce lagrangien fait intervenir des équation aux dérivées partielles, dont l'existence ou l'unicité des solutions est inconnue dans le cas général. On peut toutefois, en imposant certaines conditions initiales, lever ce problème. Néanmoins, cela n'est pas satisfaisant d'un point de vue physique, car de telles conditions ne correspondent pas (ou ne permettent pas de se ramener) à celles de l'expérience.
Extensions aux autres forces
Les premières équations de Yang-Mills à être introduites étaient les équations de Yang-Mills pour l'électromagnétisme, qui remplacent celles de Maxwell :
ou dA est l'extension covariante de jauge de la dérivée extérieure,
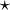l'étoile de Hodge et enfin J est le terme de sources. Il apparaît, par opposition aux équations de Maxwell, que les équations de Yang-Mills ne sont pas linéaires. Ainsi, seules quelques solutions exactes à ces équations sont connues, la plupart du temps sous forme d’ansatz.Le succès de la théorie de Yang-Mills avec l'électromagnétisme amena à se poser la question de son efficacité éventuelle à traiter les deux autres forces quantiques : l'interaction nucléaire faible et forte. Cependant, la théorie utilise des vecteurs d'interaction de masse nulle : cela fonctionne pour l'électromagnétisme, dont le vecteur est le photon. Mais cela fut un obstacle pour les deux interactions nucléaires, dont on savait qu'au moins une partie était transmise par des bosons massifs.
La compréhension du mécanisme de Higgs, qui donne une masse aux vecteurs des interactions nucléaires, et de l'unification électro-faible, qui réunit électromagnétisme et interaction faible dans une même description théorique, constituèrent les deux principaux éléments à partir desquels la théorie de Yang-Mills put s'appliquer à ces deux interactions quantiques.
L'interaction forte révéla en fait une propriété remarquable de la théorie de Yang-Mills elle-même : la liberté asymptotique. Cela permit la description de cette interaction dans SU(3) au travers de la chromodynamique quantique, qui utilise les mêmes concepts.
Le problème du gap de masse
Cependant, la description de l'interaction forte faite par cette théorie ne peut vérifier l'expérience que si elle présente un certain nombre de phénomènes purement quantiques :
- Elle doit posséder un « gap de masse » : il doit exister une constante (par nature positive) telle que toute excitation du vide soit d'énergie au moins cette constante. Cela explique pourquoi cette interaction est si forte et de portée si courte.
- Elle doit expliquer le « confinement de couleur » : la théorie s'exprime dans SU(3), mais les particules comme les protons ou les neutrons sont invariants dans ce groupe. En effet, on n'observe jamais de quark individuellement.
- Elle doit permettre la « brisure de symétrie chirale », afin de rester cohérente avec les descriptions algébriques des pions.
Ces propriétés, bien qu'observées dans les simulations ou dans les accélérateurs de particules, ne sont pas encore comprises dans la théorie de Yang-Mills. On peut parfois les expliquer dans des modèles extrêmement simplifiés, mais ces preuves ne s'étendent pas à la théorie complète.
Annexes
Bibliographie
- (en) P. Deligne, P. Etingof, D. Freed, L. Jeff rey, D. Kazhdan, J. Morgan, D. Morrison, E. Witten, Quantum Fields and Strings: A Course for Mathematicians, American Mathematical Society, Providence, RI, 1999, p. XXX.
- (en) N. A. Nekrasov : « Seiberg-Witten prepotential from instanton counting ». Proceedings of the ICM, Beijing 2002, vol. 3, 477–496 ;
- (en) N. A. Nekrasov, A. Okounkov : « Seiberg-Witten Theory and Random Partitions » ;
- (en) J. A. Minahan, K. Zarembo : « The Bethe-Ansatz for N=4 Super Yang-Mills ». JHEP 0303 (2003) 013 ;
- (en) V.A.Kazakov, A.Marshakov, J.A.Minahan, K.Zarembo : « Classical/quantum integrability in AdS/CFT ».
Notes et références
- ↑ L'électromagnétisme, basée sur le groupe abélien U(1) n'est pas une théorie de Yang-Mills car elle est abélienne mais sa formulation fournit un modèle pour l'ensemble des théories de Yang-Mills, qui en sont ainsi une généralisation.
- ↑ Seules certaines théories dites libres, c'est-à-dire sans interaction et donc plus simples, ont vu leur existence démontrée dans le cadre de la théorie constructive des champs.
- ↑ (en) Yang-Mills and Mass Gap, Clay Mathematics Institute.
- ↑ Un tel espace est appelé un fibré principal.
- ↑ L'étude des connexions peut se faire de façon plus générale sur l'ensemble des variétés différentielles. Dans le cas des variétés riemanniennes, c'est-à-dire les variétés possédant une métrique, on peut considérer la connexion de Levi-Civita qui joue un rôle central en relativité générale.
Voir aussi
Liens externes
Problèmes du prix du millénaire Hypothèse de Riemann - Conjecture de Poincaré - P=NP - Conjecture de Hodge - Conjecture de Birch et Swinnerton-Dyer - Équations de Navier-Stokes - Équations de Yang-Mills 
Portail des mathématiques
Portail de la physique
Catégories : Problèmes du prix du millénaire | Théorie quantique des champs | Électrodynamique quantique
Wikimedia Foundation. 2010.
